机器学习实战(二)
基础数学知识
机器学习中的函数
**机器学习基本上等价于寻找函数的过程。**机器学习的目的是进行预测、判断,实现某种功能。通过学习训练集中的数据,计算机得到一个从x到y的拟合结果,也就是函数。例如:
除了线性函数(一次函数)、二次函数、多次函数和对数函数以外,机器学习中有一种很重要的函数:激活函数。
激活函数(activation function)
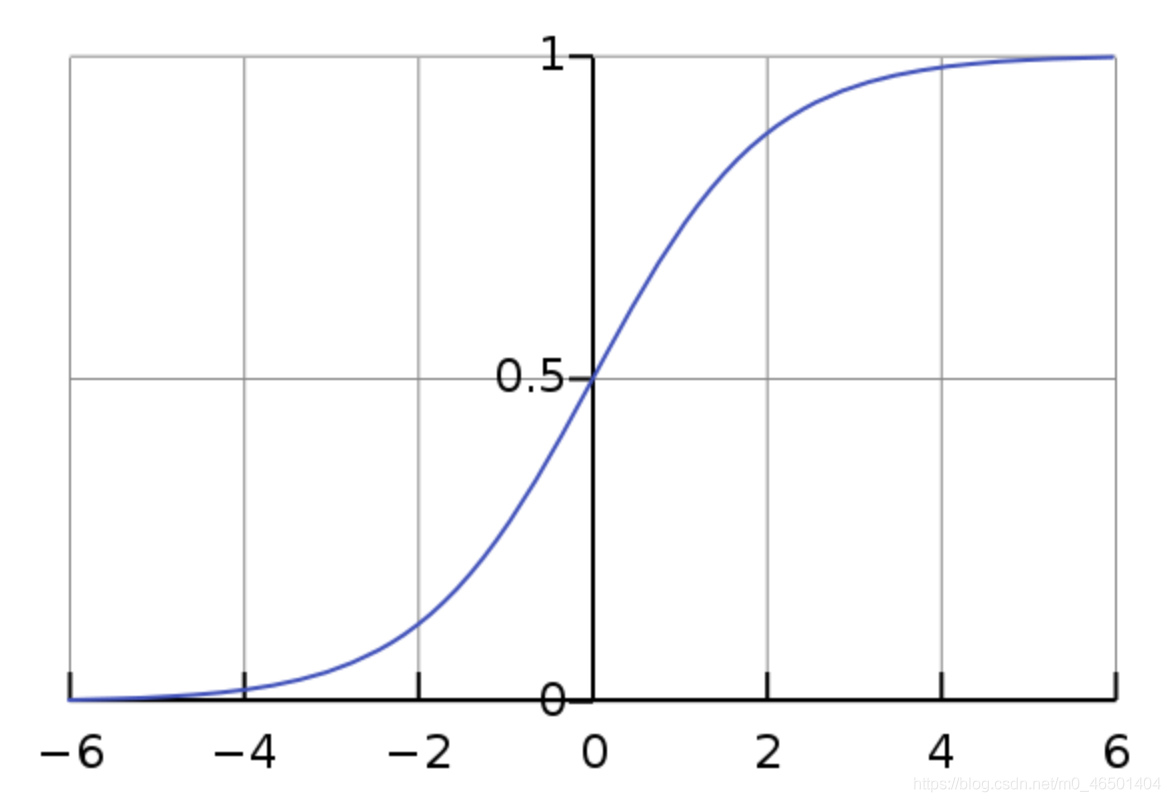
激活函数的作用是在学习算法中实现非线性的、阶跃性质的变换,其中最常见的是Sigmoid函数。
函数凹凸性
凸函数是只存在一个最低点的函数。例如如下图:
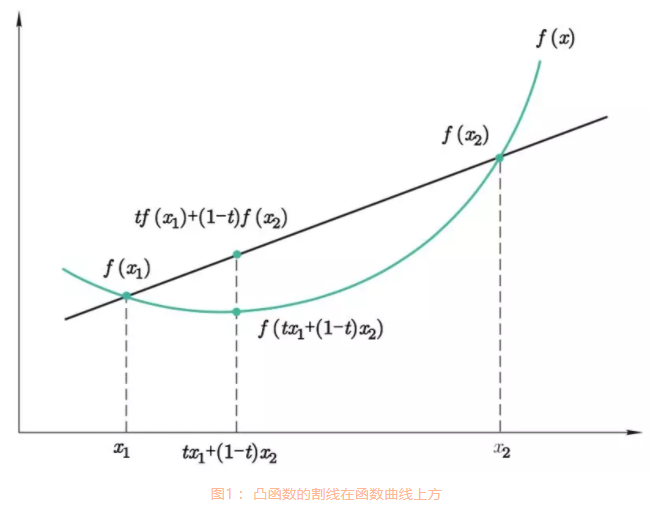
注意:在各种地方对于凸函数和凹函数的定义不同,方向可能会相反,但是因为函数概念和机器学习概念最初都是国外来的,因此我们遵循国外的习惯,即:函数长这样 U 叫做凸函数。
想象有一个小球在凸函数上滚动,它最后就会滚到最低点,别的函数都做不到。达到全局最低点就是我们在机器学习中理想的情况。
梯度下降
什么是梯度?
对多元函数的各函数求偏导,然后把所求的各个参数的偏导数以向量形式写出来,就是梯度。
计算梯度向量的意义在于其函数变化的方向,而且是变化最快的方向。
下山的隐喻
在机器学习中用下山来比喻梯度下降是很常见的。想象一个人在山上,想知道如何下山,只能一步一步往下走,在一个位置求这个位置的梯度,然后沿着梯度的负方向也就是最陡峭的地方向下走一步,然后再求新位置的梯度,循环往复,直到走到山脚。如果此时这座山不是凸函数的话,也许这个人在山腰处就卡住了,以为那里就是山脚。(局部最优解)
梯度下降的用处。简单的说,有以下几点:
- 机器学习的本质是找到最优的函数。
- 如何衡量函数是否优化?其方法是尽量减少预测值和真值之间的误差(损失值)
- 可以建立误差和模型参数之间的函数(最好是凸函数)
- 梯度下降能够引导我们走到凸函数的全局最低点,也就是误差最少的时候。
机器学习的数据结构——张量(tensor)
张量的轴、阶、形状
这一块内容非常重要,因为在机器学习中,我们常常会接触到张量。
张量是机器学习程序中的数字容器,本质上就是各种不同维度的数组。张量的维度称之为轴(axis),轴的个数称为阶(rank)(阶就是俗语的维度,但是请务必注意其不同)。
张量的形状(shape)就是张量的阶,加上每个阶的维度。
这是我对于张量的理解,阶的维度其实就是阶的长度。
标量——0D(阶)张量
仅包含一个数字的张量叫标量(scalar)。
利用numpy创建一个标量。
1 | import numpy as np # 后续代码省略导入numpy库 |
输出结果为:
1 | X的值: 5 |
- 注意在这里我们就把它称为一个数,而不是一个“有一个数的向量”,这是不同的,就像 $ \bold{1(数) \neq (1)(矩阵))} $。因为一个数没有轴,即轴个数为0,轴长度也就没什么意义了,所以X的形状就是(),空的,啥也没有。可以把“()”理解成张量的标志。
向量——1D(阶)张量
那么显然,向量(vector)是一串数字了,就比孤孤单单的一个数多了一个轴,而且这个轴也有长度了。
1 | X = np.array([1,2,3,4,5]) |
1 | X的值: [1 2 3 4 5] |
- 注意,分析以下这时候X的形状,()表示是个张量,里面有一个数字,表示它是1阶,数字为5,表示这一阶的维度(长度)为5。(有5个数呀)
向量的点积
我们直到,两个向量可以做点积,中学都学过的:
代码实现:
1 | X = np.array([1,2,3,4,5]) |
- 向量乘积遵循交换律: $ \vec A\vec B = \vec B\vec A $
矩阵——2D(阶)张量
矩阵(matrix)是一组一组向量的集合。矩阵就是2阶张量,它的形状为(样本,特征)。其表现形式为:
| 特征1 | 特征2 | …… | 特征n | |
|---|---|---|---|---|
| 样本1 | 数据(1,1) | 数据(1,2) | …… | 数据(1,n) |
| 样本2 | 数据(2,1) | …… | …… | …… |
| …… | …… | …… | …… | …… |
| 样本n | 数据(n,1) | …… | …… | 数据(n,n) |
矩阵的点积
矩阵也可以进行点积,需满足矩阵乘法规则。这里具体就不说了。
序列数据——3D(阶)张量
如果说2D张量就像表格一样,那3D张量就很像多张表格叠在一起。在上一篇博客中,我们处理过MNIST数据集,实际上MNIST数据集是4D张量,因为图片会有一层深度信息,例如RGB就是三通道,深度为3,但是MNIST为灰度图像,只有1层深度,所以理论上可以把它当作3D张量处理。序列数据集才是真正的3D张量,其中最常见的是时间序列(time series)
其结构为:
- 第一个轴:样本轴
- 第二个轴:时间步轴
- 第三个轴:特征轴
例如我记录杭州一个月的天气情况。特征包含(温度、湿度、风力),样本包含(1月1日,1月2日,……,1月30日),时间步长设定为:每30分钟测量一次上述的几个特征。就是这个意思,应该好理解。
也就是说,时许数据集的形状为:(样本,时戳,标签)
图像数据——4D张量
刚才已经提到了,MNIST实际上就是4D张量。因为一张图片就有三个维度了,长、宽、通道数。
视频数据——5D张量
显而易见,视频又加了一维时间,但这个时间是用帧数来表示的,所以视频数据张量结构里比图像数据多了一维“帧”。
通过索引和切片访问张量中的数据
索引好理解,就像数组里面我们调用一个元素,会使用a[n]这样的方式。切片比较特殊,如果接触过matlab那么对这个用法会比较熟悉。下面看代码示例:
1 | array = np.arange(10) |
再给出一个有点复杂的例子:
1 | array = np.array([[1,2,3],[4,5,6]]) |
- 看起来同样是4,5,6,但第一条是两个括号括起来的,里面的[4,5,6]实际上是一个整体,而第二条就是三个元素。两者阶数不相同。张量是机器学习的数据结构,其形状是数据处理的关键!
张量的整体操作和逐元素运算
张量的加减乘除乘方都可以整体进行或者逐元素进行。
1 | array = np.array([1,2,3]) |
张量的变形和转置
使用reshape方法进行变形和转置,T方法进行转置
1 | array = np.array([[1,2,3],[4,5,6]]) |
- 注意,调用reshape方法和T方法时,原array并没有变,要通过赋值才能改变原array的值
- 注意,调用reshape的时候一定要保证数据个数乘起来时一样的,不然会报错。
广播
Python的广播功能是numpy对形状不完全相同的数组间进行计算的方式。给出示例代码:
1 | array_1 = np.array([[0,0,0],[10,10,10],[20,20,20],[30,30,30]]) |
1 | array_2的形状: (1, 3) |
机器学习的几何意义
机器学习的向量空间
张量,可以被解释为某种几何空间内点的坐标。这样,机器学习中特征向量就形成了特征空间。考虑一个二维向量:A=(0.5, 1).我们可以把它想成一个二维坐标系的一个点。而更高维度的张量实际可以把它想象成更高维度的点。
推而广之:**机器学习模型是在更高维度的几何空间中对特征向量进行操作、变形,计算其间的距离,并寻找从特征向量到标签之间的函数拟合——这就是从几何角度所阐述的机器学习本质。
几种常见的的机器学习模型都可以通过特征空间进行几何描述。
- 回归模型:需要找到最合适的方式去拟合样本空间
- 分类模型:找到一个分割超平面将特征空间分成两个类
- 聚类模型:通过对特征空间中的特征实施某种相似性的度量,将相近的特征聚在一起。
深度学习和数据流形
深度学习的过程实际上就是数据提纯的过程。主要因为特征维度过高,导致特征空间十分复杂,进而导致机器学习建模难度过大。有一种是通过流形(manifold)学习将高维特征空间中的样本分布群“平铺”至一个低维空间,同时能保存原高维空间中样本点之间的局部位置的相关信息。
在传统的机器学习中,流形学习主要用于特征提取和数据降维,特征提取使特征变得更加友好,降维是因为高维数据通常有冗余。
而在深度学习出现之后,有一种说法认为神经网络能够自动自发地将复杂的特征数据流形展开,从而减少了特征提取的需要。
就像一张写了很多信息的纸但是揉皱了,我们只需要把它展开读取信息就行。
因此,现代的深度神经网络(DNN)通过参数学习,展开了高维数据的流形——这可以说是深度学习的几何意义。
课后练习
一 变量(x, y)的集合{(-5, 1),(3, -3),(4, 0),(3, 0),(-4, 3)}是否满足函数的定义?为什么?
答:满足。因为x与y一一对应,且没有同一个x值对应两个y。
二 画出线性函数y=2x+1的函数图像,并在图中标出其斜率和y轴上的截距
答:斜率2,截距1
1 | import numpy as np |
三 在上一节中,我们曾使用语句from keras.datasets import boston_house导入了波士顿房价数据集。请同学们输出这个房价数据集对应的数据张量,并说出这个张量的形状。
四 对波士顿房价数据集的数据张量进行切片操作,输出其中第101~200个数据样本。
三四答:
1 | from keras.datasets import boston_housing |
1 | 数据集张量形状: (404, 13) |
用python生成形状如下的两个张量,确定其阶的个数,并进行点积操作,最后输出结果。
A = [1, 2, 3, 4, 5]
B = [[5],[4],[3],[2],[1]]
1 | import numpy as np |