线性回归——预测网店的销售额
问题定义
张三在运营一个网店,他发现网店商品的销量和广告推广的力度息息相关。张三准备好了以下几个问题亟待解决:
(1)各种广告和商品销售额的相关度如何?
(2)各种广告和商品销售额之间体现出一种什么关系?
(3)哪一种广告对于商品销售额影响最大?
(4)分配特定的广告投放金额,预测出未来的商品销售额。
数据的收集和预处理
收集网店销售额数据
已经收集好的销售额的数据,在数据集中主要包含以下内容:
数据读取和可视化
首先进行数据可视化 的工作,先要对这份数据有个直观的了解。
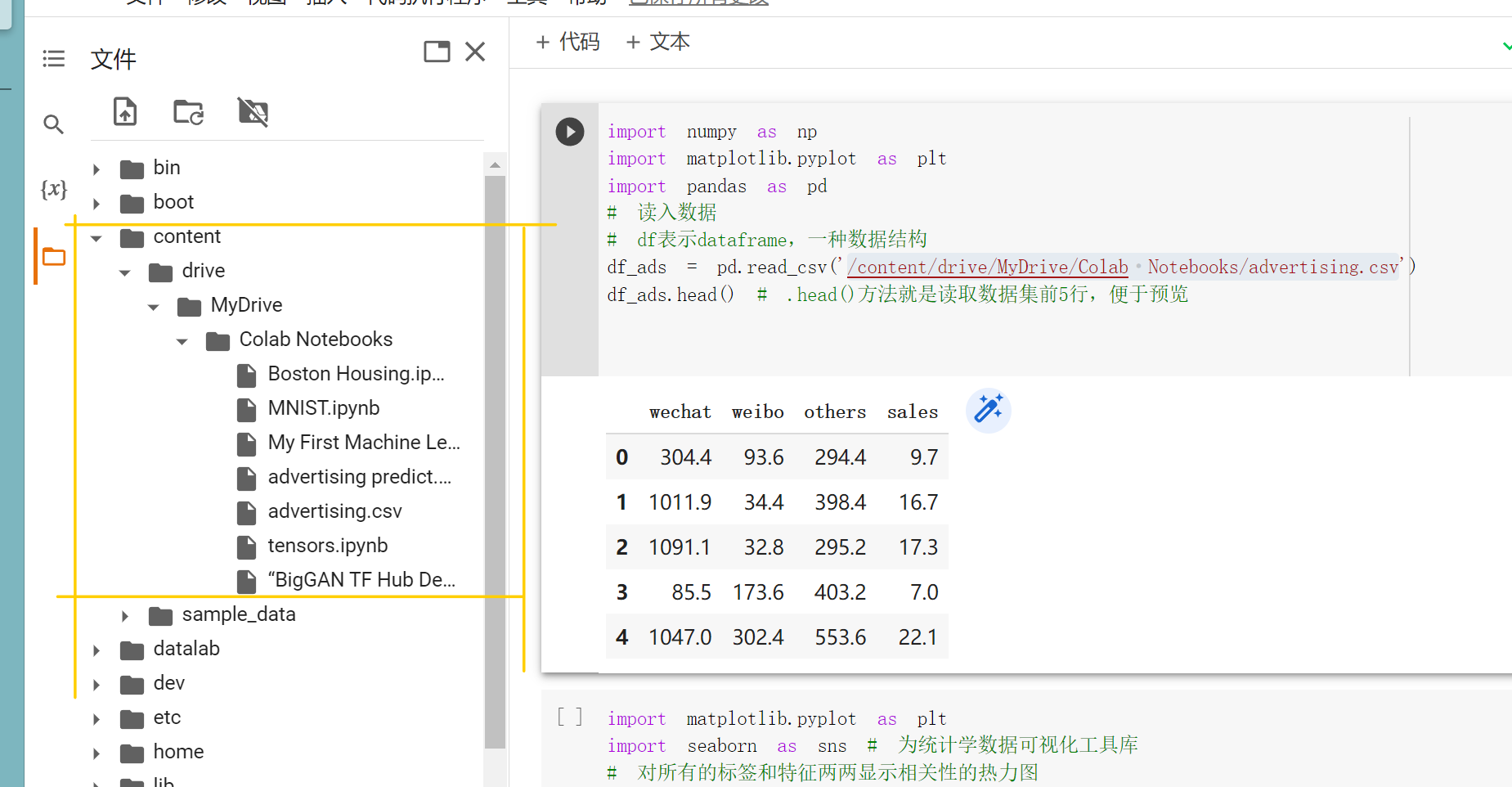
1 2 3 4 5 6 7 import numpy as npimport pandas as pdimport matplotlib.pyplot as pltdf_ads = pd.read_csv(/content/drive/MyDrive/Colab Notebooks/advertising.csv) df_ads.head()
结果如下:
1 2 3 4 5 6 wechat weibo others sales 0 304.4 93.6 294.4 9.7 1 1011.9 34.4 398.4 16.7 2 1091.1 32.8 295.2 17.3 3 85.5 173.6 403.2 7.0 4 1047.0 302.4 553.6 22.1
使用colab时,我们将数据集文件上传到和.ipynb文件同目录下,但是不能使用pd.read_csv(‘advertising.csv’),我们可以在笔记本文件内部左侧的文件树中找到我们想要的文件目录。
数据的相关分析
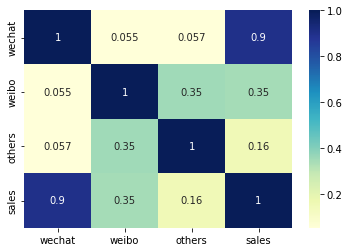
相关分析 (correlation analysis)后我们可以通过相关性系数了解数据集中任意一对变量(a, b)间的相关性。相关性系数是一个-1~1的值,正值表示正相关的,负值表示负相关,如果a和b的相关系数是1,则a和b总是相等的。热力图 (heatmap)的方式非常直观的地展示出来。
1 2 3 import seaborn as sns sns.heatmap(df_ads.corr(), cmap='YlGnBu' , annot=True ) plt.show()
从热力图结果来看,将资金投放在微信上对销售额影响最大,因此应该多投资微信广告
数据散点图
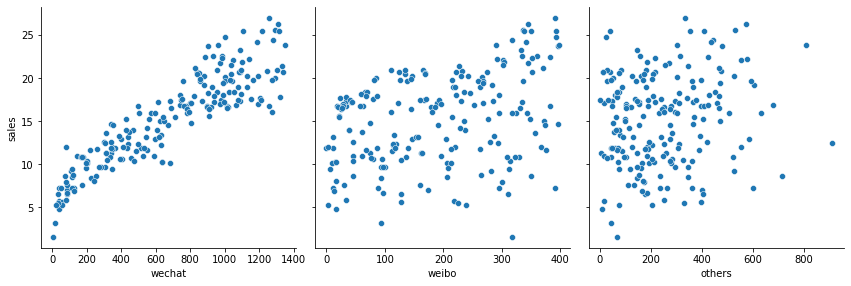
通过散点图(scatter plot)两两一组显示商品销售额和各种广告投放金额之间的对应关系。
1 2 3 4 5 sns.pairplot(df_ads, x_vars=['wechat' ,'weibo' ,'others' ],y_vars='sales' , height=4 ,aspect=1 ,kind='scatter' ) plt.show()
从这个图中我们就可以看出销售额和各种广告投资间大概的函数关系。
数据清洗和规范化
数据清洗是为了去除掉误差很大的数据或者我们不需要的数据。
下面的代码则是保留了微信相关的数据集,删去了微博和其他这两个特征段。
1 2 3 4 5 X = np.array(df_ads.wechat) y = np.array(df_ads.sales) print ("张量X的阶:" , X.ndim)print ("张量X的形状:" , X.shape)print ("张量X的内容:\n" , X)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 张量X的阶: 1 X的形状: (200,) X的内容: [ 304.4 1011.9 1091.1 85.5 1047. 940.9 1277.2 38.2 342.6 347.6 980.1 39.1 39.6 889.1 633.8 527.8 203.4 499.6 633.4 437.7 334. 1132. 841.3 435.4 627.4 599.2 321.2 571.9 758.9 799.4 314. 108.3 339.9 619.7 227.5 347.2 774.4 1003.3 60.1 88.3 1280.4 743.9 805.4 905. 76.9 1088.8 670.2 513.7 1067. 89.2 130.1 113.8 195.7 1000.1 283.5 1245.3 681.1 341.7 743. 976.9 1308.6 953.7 1196.2 488.7 1027.4 830.8 984.6 143.3 1092.5 993.7 1290.4 638.4 355.8 854.5 3.2 615.2 53.2 401.8 1348.6 78.3 1188.9 1206.7 899.1 364.9 854.9 1099.7 909.1 1293.6 311.2 411.3 881.3 1091.5 18.7 921.4 1214.4 1038.8 427.2 116.5 879.1 971. 899.1 114.2 78.3 59.6 748.5 681.6 261.6 1083.8 1322.7 753.5 1259.9 1080.2 33.2 909.1 1092.5 1208.5 766.2 467.3 611.1 202.5 24.6 442.3 1301.3 314.9 634.7 408.1 560.1 503.7 1154.8 1130.2 932.8 958.7 1044.2 1274.9 550.6 1259. 196.1 548.3 650.2 81.4 499.6 1033.8 219.8 971.4 779.4 1019.2 1141.6 994.2 986.4 1318.1 300.8 588.8 1056.1 179.7 1080.2 255.7 1011.9 941.4 928.7 167.9 271.2 822.6 1162.1 596.5 990.5 533.3 1335.9 308.5 1106.6 805.4 1002.4 347.6 443.6 389.9 642.9 243.4 841.3 35.5 85.1 784.9 428.6 173.8 1037.4 712.5 172.9 456.8 396.8 1332.7 546.9 857.2 905.9 475.9 959.1 125.1 689.3 869.5 1195.3 121.9 343.5 796.7]
对于回归问题的数值类型数据集,机器学习模型所读入的规范格式应该为2D张量,即矩阵,其形状为(样本数,标签数) ,因此我们下一步需要给张量变形。
1 2 3 4 5 X = X.reshape(len (X), 1 ) y = y.reshape(len (y), 1 ) print ("张量X的阶:" , X.ndim)print ("张量X的形状:" , X.shape)print ("张量X的内容:\n" , X)
1 2 3 4 5 6 7 8 9 10 张量X的阶: 2 X的形状: (200, 1) X的内容: [[ 304.4] [1011.9] [1091.1] ... [ 121.9] [ 343.5] [ 796.7]]
拆分数据集为训练集和测试集
在普通的机器学习项目中,至少需要包含这两个数据集,一个用于训练机器,确定模型,另一个用于测试模型的准确性。不仅如此,往往还需要一个验证集,以在最终测试之前增加验证环节。
1 2 3 from sklearn.model_selection import train_test_split(X_train, X_test, y_train, y_test) = train_test_split(X, y, test_size = 0.2 , random_state = 0 )
test_size = 0.2,表示拆分出来的测试集占总样本量的20%
train_test_split工具已经将数据集打乱顺序了
random_state用于数据集拆分过程的随机化设定。如果指定了一个整数,那么它叫做随机化种子
数据归一化
归一化是按比例的线性缩放。数据归一化之后,数据分布不变,但是都落在一个特定区间,比如(-1, 1)或者(0, 1)
x ′ = x − m i n ( x ) m a x ( x ) − m i n ( x ) x' = \cfrac{x-min(x)}{max(x) - min(x)}
x ′ = ma x ( x ) − min ( x ) x − min ( x )
1 2 3 4 5 6 7 8 9 def scalar (train, test )min = train.min (axis = 0 )max = train.max (axis = 0 )gap = max - min train -= min train /= gap test -= min test /= gap return train, test
归一化过程中的最大值、最小值、差都来自于训练集。不能使用测试集的数据进行特征缩放 。因此,可能会出现测试集中最小值比训练集小,最大值比训练集大的情况。
这样做的原因是我们把测试集当作外来数据,我们在训练数据的时候,测试集还没出现呢。
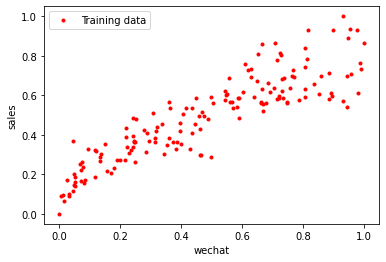
1 2 3 4 5 6 7 8 9 10 X_train, X_test = scalar(X_train, X_test) y_train, y_test = scalar(y_train, y_test) plt.plot(X_train, 'r.' , label='Training data' ) plt.xlabel('wechat' ) plt.ylabel('sales' ) plt.legend() plt.show()
选择机器学习模型
确定线性回归模型
对于此例,我们选择一元线性函数模型——y = a x + b y = ax + b y = a x + b y = w x + b y = wx + b y = w x + b y = θ 0 x + θ 1 y = \theta_0x + \theta_1 y = θ 0 x + θ 1
假设(预测)函数——h(x)
确定以线性函数作为机器学习的模型之后,我们需要介绍以下假设函数的概念。先来看一个与线性函数稍有差别的方程式:
y ′ = w x + b y' = wx + b
y ′ = w x + b
或者写成:
h ( x ) = w x + b h(x) = wx + b
h ( x ) = w x + b
y’指的是所预测出的标签,读作y帽(y-hat)或y撇。
h(x)就是机器学习所得到的函数模型,它能根据输入的特征进行标签的预测。我们把它称为假设函数 (hypothesis function)。
因为我们遇到实际问题的时候,可能不能像这个例子一样马上就确定我们要用一次函数作为模型,所以我们现在把这个例子想得复杂点,这个时候,我们就只能猜:哼~也许一次函数挺好用的吧。所以我们把这个一次函数称作假设函数。
损失(误差)函数——L(w, b)
在假定了假设函数y = w x + b y=wx+b y = w x + b 损失 (loss)的概念。(最简单的想法就是,自己找两个数带进去,然后判断好不好,拟合模型误差大不大呗)
损失,是对糟糕预测的惩罚 。损失就是误差 ,也称为成本代价 。如果模型的预测完全准确,那损失就是0。我们的目标就是0,当然,没损失几乎不可能咯。损失函数 (loss function)L ( w , b ) L(w, b) L ( w , b ) j ( θ ) j(\theta) j ( θ ) 代价函数、成本函数 )模型内部参数的评估 的过程。
用于回归的损失函数:
均方误差(Mean Square Error, MSE)函数,也叫平方损失或L2损失函数。
用于分类的损失函数:
交叉熵损失(cross-entropy loss)函数。
均方误差函数
首先,对于每一个样本,其预测值和真实值的差异为( y − y ′ ) (y - y') ( y − y ′ ) y ′ = w x + b y'=wx+b y ′ = w x + b
如果将损失值( y − y ′ ) (y-y') ( y − y ′ ) ( y − y ′ ) 2 (y-y')^2 ( y − y ′ ) 2
然后,需要把所有样本的平方损失相加,即( y ( x ( 1 ) ) − y ′ ( x ( 1 ) ) ) 2 + ( y ( x ( 2 ) ) − y ′ ( x ( 2 ) ) ) 2 + ⋅ ⋅ ⋅ + ( y ( x ( 200 ) ) − y ′ ( x ( 200 ) ) ) 2 (y(x^{(1)})-y'(x^{(1)}))^2+(y(x^{(2)})-y'(x^{(2)}))^2+···+(y(x^{(200)})-y'(x^{(200)}))^2 ( y ( x ( 1 ) ) − y ′ ( x ( 1 ) ) ) 2 + ( y ( x ( 2 ) ) − y ′ ( x ( 2 ) ) ) 2 + ⋅⋅⋅ + ( y ( x ( 200 ) ) − y ′ ( x ( 200 ) ) ) 2
∑ ( x , y ) ∈ D ( y − h ( x ) ) 2 \sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
(y-h(x))^2 ( x , y ) ∈ D ∑ ( y − h ( x ) ) 2
L ( w , b ) = M S E = 1 2 N ∑ ( x , y ) ∈ D ( y − h ( x ) ) 2 L(w,b)=MSE=\cfrac{1}{2N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
(y-h(x))^2
L ( w , b ) = MSE = 2 N 1 ( x , y ) ∈ D ∑ ( y − h ( x ) ) 2
关于以上公式,说明以上几点:
(x, y)为样本,x是特征,y是标签
h(x)是假设函数wx+b,也就是y’
D是包含多个样本的数据集
N指的是样本数量(此例中是200)。N前面还有一个常量2,是为了在求梯度的时候,抵消二次方后产生的系数,方便后续进行计算,同时增加的这个常量并不影响梯度下降的最小结果。
L是权重w和偏置b的函数,它的大小随着w和b的变化而变化。
1 2 3 4 5 6 7 def loss_function (X, y, weight, bias ): y_hat = weight * X + bias loss = y - y_hat cost = np.sum (loss**2 )/(2 *len (X)) return cost print ("当权重为5,偏置为3时,损失为:" , loss_function(X_train, y_train, weight=5 , bias=3 ))print ("当权重为100,偏置为1时,损失为:" , loss_function(X_train, y_train, weight=100 , bias=1 ))
1 2 当权重为5,偏置为3时,损失为: 12.796390970780058 当权重为100,偏置为1时,损失为: 1577.9592615030556
因此我们可以说,y = 3 x + 5 y=3x+5 y = 3 x + 5 y = 100 x + 1 y=100x+1 y = 100 x + 1
为什么说我们要用( y − y ′ ) 2 (y-y')^2 ( y − y ′ ) 2 之所以平方,是为了让L(w, b)形成相对于w和b的凸函数,从而实现梯度下降
通过梯度下降找到最佳参数
上部分我们自己定义了两组参数,明眼人,学过数学的,都能看出来(3,5)要比(100,1)好吧!但是机器就是呆呆的,只能通过损失函数判断。那我们要怎么去找一组最理想的参数(w,b)呢?显然,利用电脑算的比人快不知道多少的优点,我们可以让机器随机生成一亿组参数,每组都算一下loss,然后从小到大排一下,不就找到了一亿组参数中效果最好的参数了嘛,大差不差也算找到了。也不是不行 ,但是这显然有点low,而且计算量大,毫无目的性可言,就像无头苍蝇到处乱撞。因此,理想的情况是,每一次生成参数、猜测都应该比上一次要好,我们让参数(w,b)逐渐变好不就行了嘛 ,那么怎么做呢,这就要用到梯度下降 了。
凸函数确保有最小损失点
梯度下降就是我们寻找最优参数的方向 ,而光有方向还不够,我们还需要知道什么时候停止。
L ( w , b ) = M S E = 1 2 N ∑ ( x , y ) ∈ D ( y − ( w x + b ) ) 2 L(w,b)=MSE=\cfrac{1}{2N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
(y-(wx+b))^2
L ( w , b ) = MSE = 2 N 1 ( x , y ) ∈ D ∑ ( y − ( w x + b ) ) 2
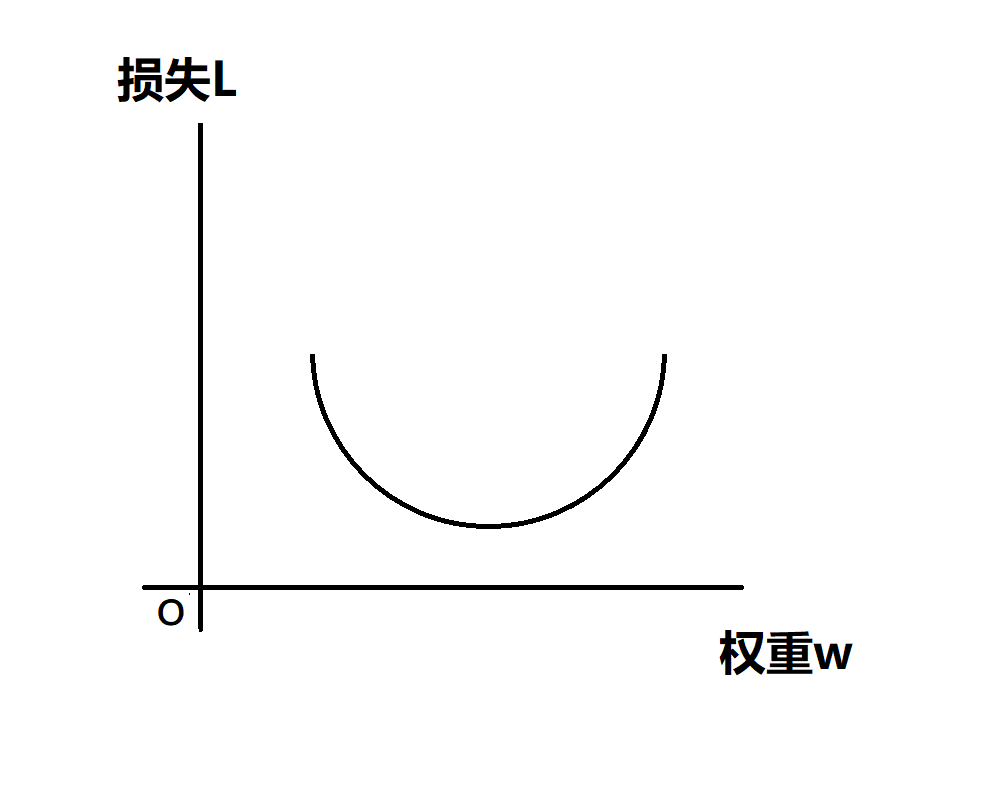
这个函数的图像大概如下:
我们将这个图像称为损失曲线,是一个凸函数,其存在一个全局最小损失点
梯度下降的实现
例如此时我们要找w的最优值,而现在w=5,接下来我们要让w=5.01还是4.99呢,当然,如果你看到了函数图像,你可能就知道它要向数轴哪边移动了。如果我们看不到图像,怎么办呢?这就需要我们高数中的知识了:求导!
如果求导之后梯度为正值,则说明L正在随着w增大而增大,应该减小w
如果求导之后梯度为负值,则说明L正在随着w增大而减小,应该增大w
用数学语言描述如下:
梯度 = { ∂ ∂ w 1 2 N ∑ ( x , y ) ∈ D ( y − ( w ⋅ x + b ) ) 2 = 1 N ∑ ( x , y ) ∈ D ( ( w ⋅ x + b ) − y ) ⋅ x ∂ ∂ b 1 2 N ∑ ( x , y ) ∈ D ( y − ( w ⋅ x + b ) ) 2 = 1 N ∑ ( x , y ) ∈ D ( ( w ⋅ x + b ) − y ) 梯度=
\begin{cases}
\cfrac{\partial}{\partial w}\cfrac{1}{2N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
(y-(w \cdot x+b))^2 =
\cfrac{1}{N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
((w \cdot x+b)-y)\cdot x \\
\\
\cfrac{\partial}{\partial b}\cfrac{1}{2N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
(y-(w \cdot x+b))^2 =
\cfrac{1}{N}
\sum_{
\begin{subarray}{}
(x,y) \in D
\end{subarray}}
((w \cdot x+b)-y) \\
\end{cases}
梯度 = ⎩ ⎨ ⎧ ∂ w ∂ 2 N 1 ∑ ( x , y ) ∈ D ( y − ( w ⋅ x + b ) ) 2 = N 1 ∑ ( x , y ) ∈ D (( w ⋅ x + b ) − y ) ⋅ x ∂ b ∂ 2 N 1 ∑ ( x , y ) ∈ D ( y − ( w ⋅ x + b ) ) 2 = N 1 ∑ ( x , y ) ∈ D (( w ⋅ x + b ) − y )
利用代码写出公式(这段代码不用写在notebook中):
1 2 3 4 y_hat = weight*X+bias loss = y_hat-y derivative_weight = X.T.dot(loss)/len (X) derivative_bias = sum (loss)*1 /len (X)
对偏置b求导并不需要与特征X相乘,因为偏置与权重不同,它与特征并不相关。另外还有一种思路,是把偏置看作w 0 w_0 w 0 X 0 X_0 X 0
确保学习速率
学习速率就是指以多快的速度下山。学习速率(learning rate)也记作α 。
w = w − α ⋅ ∂ ∂ w L ( w ) w=w-\alpha \cdot \cfrac{\partial}{\partial w}L(w)
w = w − α ⋅ ∂ w ∂ L ( w )
1 2 weight = weight - alpha * derivative_weight bias = bias - alpha * derivative_bias
α是一个超参数
显然,如果α太小,机器学习的速度会很慢,如果α太大,可能会容易越过最低点。
下面给出梯度下降的完整代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 def gradient_descent (X, y, w, b, lr, iter ): l_history = np.zeros(iter ) w_history = np.zeros(iter ) b_history = np.zeros(iter ) for i in range (iter ): y_hat = w * X + b loss = y_hat - y derivative_w = X.T.dot(loss)/len (X) derivative_b = sum (loss)*1 /len (X) w = w - lr * derivative_w b = b - lr * derivative_b l_history = loss_function(X, y, w, b) w_history = w b_history = b return l_history, w_history, b_history
实现一元线性回归模型并调试超参数
设定初始值
1 2 3 4 5 6 7 8 9 iteration = 100 alpha = 1 weight = -5 bias = 3 print ('当前损失:' , loss_function(X_train, y_train, weight, bias))
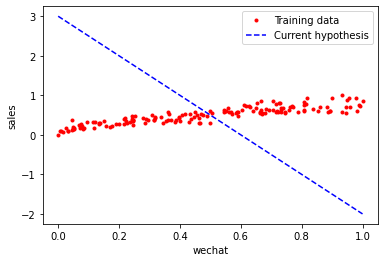
下面画出当前回归函数的图像:
1 2 3 4 5 6 7 8 plt.plot(X_train, y_train, 'r.' , label='Training data' ) line_X = np.linspace(X_train.min (), X_train.max (), 500 ) line_y = [weight * xx + bias for xx in line_X] plt.plot(line_X, line_y, 'b--' , label='Current hypothesis' ) plt.xlabel('wechat' ) plt.ylabel('sales' ) plt.legend() plt.show()
输出图像如下所示:
将初始假设函数设定如此“离谱”,是为了让人直观看到后面梯度下降的过程和变化。
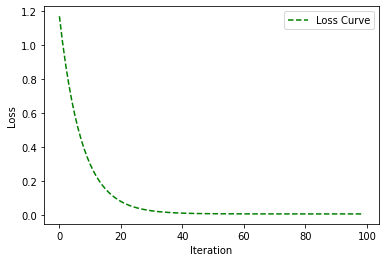
进行梯度下降
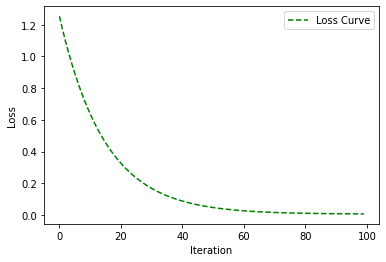
1 2 3 4 5 6 7 8 9 loss_history, weight_history, bias_history = gradient_descent(X_train, y_train, weight, bias, alpha, iteration) plt.plot(loss_history, 'g--' , label='Loss Curve' ) plt.xlabel('Iteration' ) plt.ylabel('Loss' ) plt.legend() plt.show()
如图:
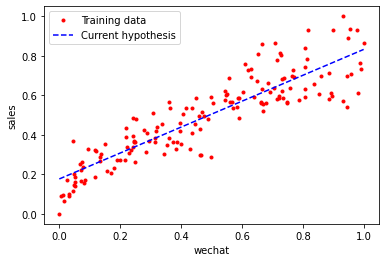
1 2 3 4 5 6 7 8 9 plt.plot(X_train, y_train, 'r.' , label='Training data' ) line_X=np.linspace(X_train.min (), y_train.min (), 500 ) line_y = [weight_history[-1 ] * xx + bias_history[-1 ] for xx in line_X] plt.plot(line_X, line_y, 'b--' , label='Current hypothesis' ) plt.xlabel('wechat' ) plt.ylabel('sales' ) plt.legend() plt.show()
如图:
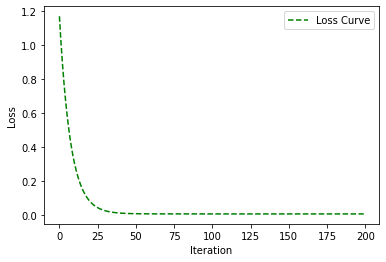
调试超参数
超参数作为函数外部的参数,也是可以很大程度上影响学习结果的。显而易见,迭代次数越多,效果就越来越好,但是可能由于边际效益,后面的训练可能也没什么必要了。
1 α=0.5,iteration=100时:
2 α=1,iteration=200时:
下面输出α=1,iteration=100时的参数值:
1 2 3 4 print ("当前损失:" ,loss_function(X_train, y_train, weight_history[-1 ], bias_history[-1 ])) print ("当前权重:" , weight_history[-1 ])print ("当前偏置:" , bias_history[-1 ])
1 2 3 当前损失: 0.00465780405531404 当前权重: 0.6552253409192808 当前偏置: 0.17690341009472488
在测试集上进行预测
1 2 3 4 print ("测试集损失:" , loss_function(X_test, y_test, weight_history[-1 ], bias_history[-1 ]))
说明我们找到了一个比较好的模型!
w = 0.6552253409192808 b = 0.17690341009472488 模型: y ′ = 0.66 x + 0.17 w = 0.6552253409192808 \\ b = 0.17690341009472488 \\ 模型:y'=0.66x+0.17
w = 0.6552253409192808 b = 0.17690341009472488 模型: y ′ = 0.66 x + 0.17
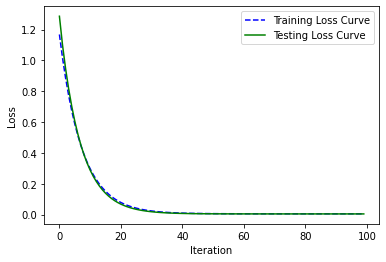
我们还可以同时显示测试集与训练集的损失曲线。
1 2 3 4 5 6 7 8 9 loss_history_tr, weight_history_tr, bias_history_tr = gradient_descent(X_train, y_train, weight, bias, alpha, iteration) loss_history_te, weight_history_te, bias_history_te = gradient_descent(X_test, y_test, weight, bias, alpha, iteration) plt.plot(loss_history_tr, 'b--' , label='Training Loss Curve' ) plt.plot(loss_history_te, 'g-' , label='Testing Loss Curve' ) plt.xlabel('Iteration' ) plt.ylabel('Loss' ) plt.legend() plt.show()
如图:
由于这一章内容较多,剩下的内容放在下一节中,由于有关线性回归的内容实际上已经比较完整了,在此小作暂停。