逻辑回归——给病患和鸢尾花分类
问题定义:判断客户是否患病
机器学习主要有两大应用,一是回归问题,二是分类问题。在上节已经结束了回归算法后,这节开始我们要了解逻辑回归(logistic regression)。为什么逻辑回归也有“回归”两个字呢,因为本质上来说,逻辑回归算法也是通过调整权重w和偏置b来找到找到线性函数来计算数据样本属于某一类的概率。
现在有这样一个实际问题:我们现在因实际需要,想要知道一个人的心脏健康状况,例如一个人有心脏病的可能性。在研究这个问题之前,我们首先需要查看大量医院心脏病例的大量资料,查看可能导致心脏病的因素,比如先天因素,后天因素等。现在呢假设我们已经有个1000个人的资料了,然后我们从统计和经验出发,归纳出几个可能会影响心脏病的因素:
——————————
- age: 年龄
- sex: 性别
- cp: 胸痛类型
- trestbps: 休息时血压
- chol: 胆固醇
- fbs: 血糖
- restecg: 心电图
- thalach: 最大心率
- exang: 运动后心绞痛
- oldpeak: 运动后ST段压低
- slope: 运动高峰期ST段的斜率
- ca: 主动脉荧光造影染色数
- thal: 缺陷种类
- target: 0代表有无心脏病,1代表有心脏病
——————————
也就是说,target是我们要调查的目标,也就是标签。其他的特征。
在收集到的数据中,要注意,有的人target是1,也就是有心脏病,有的人是0,但还有些人是空白,他们可能自己也不知道有没有心脏病。这些数据就是无标签的数据。
从回归问题到分类问题
其实从回归问题到分类问题,可以直观感受到,问题的解决领域是从连续到离散的。回归问题要求我们拟合一个连续的函数,而分类问题要求我们输出一个明确的类别。在输出明确的离散分类值之前,算法首先输出的其实是一个可能性,可以把这个可能性理解成一个概率。
- 机器学习模型根据输入数据判断一个人患心脏病的可能性为80%,那么就把这个人判定为“患病”类,输出1。
- 机器学习模型根据输入数据判断一个人患心脏病的可能性为30%,那么就把这个人判定为“健康”类,输出0。
用线性回归+阶跃函数完成分类
这一节图例较多,强烈建议大家去看一下书中的原内容,讲的很简单易懂!
我们这里拿一个例子打比方:考试。
**考试没到60分则输出0,表示不及格;60分以上则输出1,表示及格。**因此统计图大概如下:

这种图你要画一条什么函数去拟合呢?显然不可能是一次函数吧!二次函数好像也不行……总而言之,我们找到了下面这样一条函数:
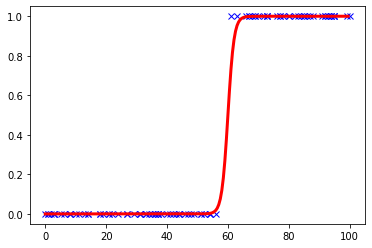
它的名字叫sigmoid函数,是阶跃函数的一种。书中还讲到了一种拟合方法,是将回归函数到转换成分段函数进行拟合,但是比较容易受误差过大的数据的影响,这里就不介绍了。
sigmoid函数的公式如下:
f(x)=1+e−x1
逻辑函数的假设函数
有了sigmoid函数,就可以开始正式建立逻辑回归的机器学习模型。重点要确定假设函数h(x),来预测y’。
总结以下之前的内容,把线性回归和逻辑函数整合起来,形成逻辑回归的假设函数。
(1)首先通过线性回归模型求出一个中间值z,z=w0x0+w1x1+...+wnxn=WTX。它是一个连续值,区间并不在[0, 1]之间,可能小于0或者大于1,范围从无穷小到无穷大。
(2)然后通过逻辑函数把这个中间值z转化成0~1的概率值,以提高拟合效果f(x)=1+e−x1
(3)结合步骤(1)和(2),把新的函数表示为假设函数的形式:
h(x)=1+e−(WTX)1
这个值也就是逻辑回归算法得到的y’。
(4)最后还要根据y’所代表的概率,确定分类结果。
如果h(x)>=0.5,分类结果为1
如果h(X)<0.5,分类结果为0
上述过程的关键在于选择Sigmoid函数进行从线性回归到逻辑回归的转换。Sigmoid函数的优点如下:
- Sigmoid函数是连续函数,具有单调递增性(类似于递增的线性函数)。
- Sigmoid函数具有可微性,可以进行微分,也可以进行求导。
- 输出范围为[0, 1],结果可以表示为概率的形式,为分类做出准备。
- 抑制分类的两边,对中间区域的细微变化敏感,这对分类结果拟合效果好。
逻辑回归的损失函数
把训练集中所有的预测所得概率和实际结果的差异求和,并取平均值,就可以得到平均误差,这就是逻辑回归的损失函数:
L(w,b)=N1(x,y)∈D∑Loss(h(x),y)
在逻辑回归中,我们不能使用线性回归中的损失函数MSE(均方误差函数),因为在逻辑回归中,MSE对于w和b而言不再是一个凸函数,无法使用梯度下降。
为了避免陷入局部最低点,我们为逻辑回归选择了符合条件的新的损失函数,公式如下:
{y=1,Loss(h(x),y)=−log(h(x))y=0,Loss(h(x),y)=−log(1−h(x))
整合得到损失函数如下:
L(w,b)=N−1(x,y)∈D∑[ylog(h(x))+(1−y)log(1−h(x))]
逻辑回归的梯度下降
逻辑回归的梯度下降和线性回归一样,也是先进行微分,然后把计算出来的导数乘以学习速率α,通过不断的迭代,更新w和b,直至收敛。
梯度计算公式如下:
梯度=h′(x)=∂w∂L(w,b)=∂w∂{N−1(x,y)∈D∑[ylog(h(x))+(1−y)log(1−h(x))]}
计算得到最终结果:
梯度=N1i=1∑N(y(i)−(w⋅x(i)))⋅x(i)
引入学习速率之后,参数随梯度变化而更新的公式如下:
w=w−α⋅∂w∂L(w)
即
w=w−Nαi=1∑N(y(i)−(w⋅x(i)))⋅x(i)
通过逻辑回归解决二元分类问题
数据的准备与分析
数据的准备其实在一开始就已经比较完善了。
——————————
- age: 年龄
- sex: 性别
- cp: 胸痛类型
- trestbps: 休息时血压
- chol: 胆固醇
- fbs: 血糖
- restecg: 心电图
- thalach: 最大心率
- exang: 运动后心绞痛
- oldpeak: 运动后ST段压低
- slope: 运动高峰期ST段的斜率
- ca: 主动脉荧光造影染色数
- thal: 缺陷种类
- target: 0代表有无心脏病,1代表有心脏病
——————————
使用以下代码读取数据:
1
2
3
4
5
| import numpy as np
import pandas as pd
df_heart=pd.read_csv("/content/drive/MyDrive/Colab Notebooks/heart.csv")
df_heart.head()
|
用value_counts方法输出数据集中患心脏病和没有患心脏病的人数:
1
2
3
4
5
| df_heart.target.value_counts()
|
这个步骤是很有必要的。因为如果某一类别比例特别低(例如300个数据中只有3个人患病),那么这样的数据可能不适合用逻辑回归的方法作分类。
可以对某些数据进行相关性的分析,例如可以显示年龄、最大心率这两个特征与是否患病之间的关系:
1
2
3
4
5
6
7
8
9
10
11
12
| import matplotlib.pyplot as plt
plt.scatter(x=df_heart.age[df_heart.target==1],
y=df_heart.thalach[df_heart.target==1],
c='red')
plt.scatter(x=df_heart.age[df_heart.target==0],
y=df_heart.thalach[df_heart.target==0],
marker='^')
plt.legend(['Disease', 'No disease'])
plt.xlabel('Age')
plt.ylabel('Heart Rate')
plt.show()
|
输出结果如下图:
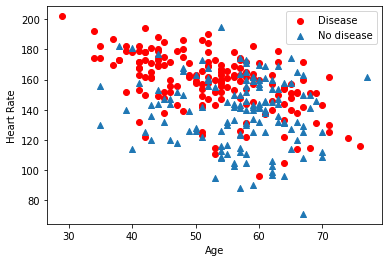
下面构建特征集和标签集:
1
2
3
4
5
6
7
| X = df_heart.drop(['target'], axis=1)
y = df_heart.target.values
print("张量X的形状:", X.shape)
print("张量y的形状:", y.shape)
|
拆分数据集:
1
2
| from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
|
数据特征缩放: 我们使用sklearn中内置的函数缩放器。
1
2
3
4
| from sklearn.preprocessing import MinMaxScalar
scalar = MinMaxScalar()
X_train = scaler.fit_transform(X_train)
X_test = scalar.transform(X_test)
|
- 这里有个点大家会发现,我们对训练集和测试集调用缩放器方法不同,一个是fit_transform(先拟合再应用),一个是transform(直接应用)。这是因为,所有的最大值、最小值、均值、标准差等数据缩放的中间值,都要从训练集得来,然后同样的值应用到训练集和测试集。 标签集已经不需要归一化了,本来就只有0&1。
建立逻辑回归模型
数据准备工作结束后,下面构建逻辑回归模型。
1.逻辑函数的定义
首先定义Sigmoid函数,一会儿会调用它:
1
2
3
4
|
def sigmoid(z):
y_hat=1/(1+np.exp(-z))
return y_hat
|
2.损失函数的定义
1
2
3
4
5
6
|
def loss_function(X,y,w,b):
y_hat = sigmoid(np.dot(X,w)+b)
loss=-((y*np,log(y_hat)+(1-y)*np.log(1-y_hat)))
cost = np.sum(loss)/X.shape[0]
return cost
|
- 在这里我们保留了b,不把它当作w0看待,所以不需要对数据集加一列1。这里的线性回归函数是多变量的,因此(X,w)点积操作之后,Sigmoid函数进行逻辑转换生成y’。
y’生成过程中需要注意的仍然是点积操作中张量X和W的形状。
- X——(242,13), 2D矩阵。
- W——(13, 1), 也是2D矩阵,因为第二阶为1,也可以看作向量
- 点积之后生成的y_hat,就是一个形状为(242,1)的张量,其中存储了每一个样本的预测值。
3.梯度下降的实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def gradient_descent(X, y, w, b, lr, iter):
l_history = np.zeros(iter)
w_history = np.zeros((iter, w.shape[0], w.shape[1]))
b_history = np.zeros(iter)
for i in range(iter):
y_hat = sigmoid(np.dot(X, w)+b)
loss = -(y*np.log(y_hat)+(1-y_hat)*np.log(1-y_hat))
derivative_w = np.dot(X.T, ((y_hat-y))/X.shape[0])
derivative_d = np.sum(loss)/X.shape[0]
w = w - lr*derivative_w
d = d - lr*derivative_b
l_history[i] = loss_function(X, y, w, b)
print("轮次", i+1, "当前轮次训练集损失:", l_history[i])
w_history[i] = w
b_history[i] = b
return l_history, w_history, b_history
|
- 这里要注意w_history是一个3D张量,因为w已经是一个2D张量了。
4.分类预测的实现
1
2
3
4
5
6
7
8
9
10
| def predict(X, w, b):
z=np.dot(X, w) + b
y_hat=sigmoid(z)
y_pred=np.zeros((y_hat.shape[0], 1))
for i in range(y_hat.shape[0]):
if y_hat[i, 0]<0.5:
y_pred[i, 0]=0
else:
y_pred[i, 0]=1
return y_pred
|
开始训练机器
1
2
3
4
5
6
7
| def logistic_regression(X, y, w, b, lr, iter):
l_history, w_history, b_history = gradient_descent(X, y, w, b, lr, iter)
print("训练最终损失:", l_history[-1])
y_pred = predict(X, w_history[-1], b_history[-1])
training_acc = 100 - np.mean(np.abs(y_pred-y_train))*100
print("逻辑回归训练准确率:{:.2f}%".format(training_acc))
return l_history, w_history, b_history
|
初始化参数:
1
2
3
4
5
6
| dimension = X.shape[1]
weight = np.full((dimension, 1), 0.1)
bias=0
alpha = 1
iterations = 500
|
调用回归模型,训练机器:
1
| loss_history, weight_history, bias_history = logistic_regression(X_train, y_train, weight, bias, alpha, iterations)
|
1
2
3
4
5
6
7
| 轮次 1 当前轮次训练集损失: 0.6151245497498954
轮次 2 当前轮次训练集损失: 0.5579913862647583
...
轮次 499 当前轮次训练集损失: 0.2932648260062251
轮次 500 当前轮次训练集损失: 0.29324449197008057
训练最终损失: 0.29324449197008057
逻辑回归训练准确率:87.19
|
测试分类结果
1
2
3
4
5
6
7
| y_pred = predict(X_test, weight_history[-1], bias_history[-1])
testing_acc = 100 - np.mean(np.abs(y_pred-y_test))*100
print("逻辑回归测试准确率:{:.2f}%".format(testing_acc))
print("逻辑回归预测分类值:", predict(X_test, weight_history[-1], bias_history[-1]))
|
绘制损失曲线
1
2
3
4
5
6
7
8
9
10
| loss_history_test = np.zeros(iterations)
for i in range(iterations):
loss_history_test[i]=loss_function(X_test, y_test, weight_historu[i], bias_history[i])
index = np.arange(0, iterations, 1)
plt.plot(index, loss_history, c='blue', linestyle='solid')
plt.plot(index, loss_history_test, c='red', linestyle='dashed')
plt.legend(["Training data", "Test Loss"])
plt.xlabel("Number of Iteration")
plt.ylabel("Cost")
plt.show()
|
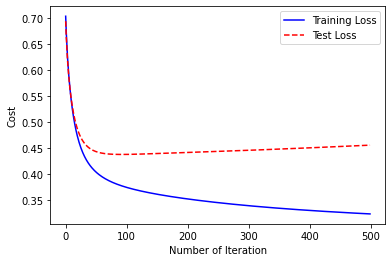
- 从图中看出,有时候损失曲线会存在上升趋势的现象,是明显的过拟合现象,因此我们要调整一下超参数。
直接调用sklearn库
直接用库的函数也可以达到同样的效果,就是我们上面这么多的工作。
1
2
3
4
5
6
| from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X_train, y_train)
print("SK learn逻辑回归测试准确率{:.2f}%".format(lr.score(X_test, y_test)*100))
|
哑特征的使用
在特征中间,有一些字段的值表示类别,比如“cp”字段,取值为1、2、3、4,这些表示的都是胸痛类型,本身不存在大小关系,但是计算机可能会觉得,4>1,意义就发生了改变。所以我们需要使用哑特征来解决这一“误解”的现象。
在构建特征值和字段值前,写如下代码:
1
2
3
4
5
6
7
8
9
|
a = pd.get_dummies(df_heart['cp'], prefix='cp')
b = pd.get_dummies(df_heart['thal'], prefix='thal')
c = pd.get_dummies(df_heart['slope'], prefix='slope')
frames= [df_heart, a, b, c]
df_heart = pd.concat(frames, axis=1)
df_heart = df_heart.drop(columns=['cp','thal','slope'])
df_heart.head()
|