问题定义：确定鸢尾花的种类（多元分类）

与第三节一样，我将多元的机器学习放在续节中。
确定鸢尾花的种类是一个经典的多分类问题。数据来自R.A. Fisher1936年发表的论文。数据集中的鸢尾花共3类，分别为山鸢尾（iris-setosa）、杂色鸢尾（iris-versicolor）、维吉尼亚鸢尾（iris-virginica）。
数据集中共有150个数据，已经按照标签类别排序，每类50个数据，其中有一类可以和其他两类进行线性的分割，但另外两类无法根据特征线性分割开。
特征和标签字段如下所示：
————————————————

  • Id: 序号
  • SepalLengthCm: 花萼长度
  • SepalWidthCm: 花萼宽度
  • PetalLengthCm: 花瓣长度
  • PetalWidthCm: 花瓣宽度
  • Species: 种类（标签）

————————————————

从二元分类到多元分类

其实从二元分类到多元分类的思想我觉得很好理解，其实就是逐个击破。每一次分类都是一次二元分类，一类接着一类分出来，而不是一下就把所有类别分好。最后一类出来的时候就是分类完成了。

多元分类的损失函数

多元分类的标签有以下两种格式：

  • 一种是one-hot格式的分类编码，比如，数字0~9分类中的数字8，格式为[0,0,0,0,0,0,0,1,0]
  • 一种是直接转换为类别数字，如1、2、3、4

因此损失函数也有以下两种情况：

  • 如果通过one-hot分类编码输出标签，则应使用分类交叉熵（categorical crossentropy）作为损失函数
  • 如果输出的标签编码为类别数字，则应使用稀疏分类交叉熵（sparse categorical crossentropy）

正则化

正则化技术是为了解决过拟合问题，这在上一节的模型中也出现了过拟合现象。如果不了解欠拟合和过拟合现象，建议看一下书，或者点击百度。

简单来说原理其实相当易懂，我们在机器学习的时候，其实是希望模型越简单越好的，谁都不想用一个100次方的函数当模型吧！虽然，如果你有100个点的话，100次方的函数一定能全给你拟合咯，但是这样的模型在用新数据的时候就会表现的很差。但是我们在面对数据的时候，咋能知道有没有过拟合呢？确实，这其实是一个无法绝对避免的问题，我们只能尽可能缓解，所以，我们的目的就是，用尽可能简单的模型做到优秀的拟合效果。所以我们可以在损失函数中加入一个惩罚项,如果模型很复杂，那这一项就变大，这样损失值就大了，强调了这次训练的“不好”;反之，模型简单就减小这项的值，表示我奖励你这个模型，在复杂度上还蛮不错哦！
正则化具体实现，我们需要引入一个模型参数λ，看一个具体例子：
加入了正则化参数之后的线性回归均方误差损失函数公式：

L(w,b)=MSE=1N∑(x,y)∈D(y−h(x))2+λ2N∑i=1nwi2L(w,b)=MSE=\cfrac{1}{N}\sum_{(x,y)\in D}(y-h(x))^2+\cfrac{\lambda}{2N}\sum_{i=1}^n w_i^2

  • 后面那一项就是正则化项，至于λ的值，可能需要手动调整。（我觉得这也是一个超参数吧）

通过逻辑回归解决多元分类问题

数据分析和准备

Sklearn自带这个数据集：

1
2
3
4
5
6
7
8
9
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

iris = datasets.load_iris() # 导入iris
X_sepal = iris.data[:, [0, 1]] # 花萼特征集：两个特征集长度和宽度
X_petal = iris.data[:, [2, 3]] # 花瓣特征集：两个特征集长度和宽度

y = iris.target

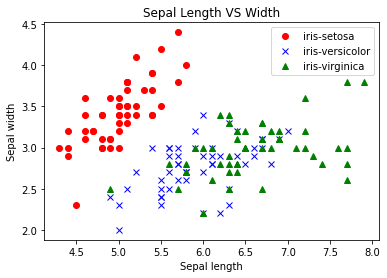
我们可以把三种鸢尾花的分类可视化：

1
2
3
4
5
6
7
8
plt.plot(iris.data[:, [0]][iris.target==0], iris.data[:, [1]][iris.target==0], 'ro')
plt.plot(iris.data[:, [0]][iris.target==1], iris.data[:, [1]][iris.target==1], 'bx')
plt.plot(iris.data[:, [0]][iris.target==2], iris.data[:, [1]][iris.target==2], 'g^')
plt.legend(["iris-setosa", "iris-versicolor", "iris-virginica"])
plt.xlabel("Sepal length")
plt.ylabel("Sepal width")
plt.title("Sepal Length VS Width")
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler # 导入标准化工具库
X_train_sepal, X_test_sepal, y_train_sepal, y_test_sepal = train_test_split(X_sepal, y, test_size=0.3, random_state=0)
print("花瓣训练集样本数：", len(X_train_sepal))
print("花瓣测试集样本数：", len(X_test_sepal))
scalar = StandardScaler()
X_train_sepal = scaler.fit_transform(X_train_sepal)
X_test_sepal = scaler.transform(X_test_sepal)

# 合并特征集和标签集，留待以后展现数据
X_combined_sepal = np.vstack((X_train_sepal, X_test_sepal))
y_combined_sepal np.hstack((y_train_sepal, y_test_sepal))

# 花瓣训练集样本数： 105
# 花瓣测试集样本数： 45

通过sklearn实现逻辑回归的多元分类

1
2
3
4
5
6
7
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(penalty='l2', C=0.1) # 设定L2正则化和C参数
lr.fit(X_train_sepal, y_train_sepal)
score = lr.score(X_test_sepal, y_test_sepal)
print("SKlearn逻辑回归测试准确率{:.2f}".format(score*100))

# SKlearn逻辑回归测试准确率68.89
  • L2正则化，只是选择了正则化的参数类别，但是用多大的力度进行呢？此时要引入另外一个配套用到正则化相关参数C。C表示正则化的力度，它与λ刚好成反比。C值越小，正则化力度越大。

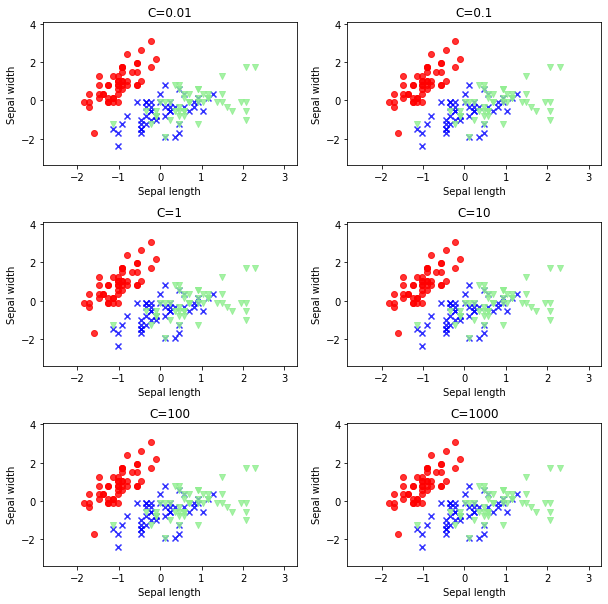
正则化参数——C值的选择

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, test_idx=None, resolution=0.02):
    markers = ('o', 'x', 'v')
    colors = ('red', 'blues', 'lightgreen')
    color_Map = ListedColormap(color[:len(np.unique(y))])
    x1_min = X[:, 0].min() - 1
    x1_max = X[:, 0].max() + 1
    x2_min = X[:, 1].min() - 1
    x2_max = X[:, 1].max() + 1
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution))
    Z = classifier.predict(np.arange([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)
    plt.contour(xx1, xx2, Z, alpha=0.4, cmap = color_Map)
    plt.xlim(xx1.min(), xx1.max())
    plt.ylim(xx2.min(), xx2.max())
    X_test, Y_test = X[test_idx, :], y[test_idx]
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl, 0], y=X[y==cl, 1], alpha=0.8, c=color_Map(idx), marker=markers[idx], label=cl)

然后使用不同的C值进行逻辑回归分类，并绘制分类结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from sklearn.metrics import accuracy_score
C_param_range = [0.01, 0.1, 1, 10, 100, 1000]
sepal_acc_tabel = pd.DataFrame(columns='C_parameter', 'Accuracy')
sepal_acc_tabel['C_parameter'] = C_param_range
plt.figure(figsize=(10,10))
j = 0
for i in C_param_range:
    lr = LogisticRegression(penalty='L2', C=i, random_state=0)
    lr.fit(X_train_sepal, y_train_sepal)
    y_pred_sepal = lr.predict(X_test_sepal)
    sepal_acc_table.iloc[j,1] = accuracy_score(y_test_sepal, y_pred_sepal)
    j += 1
    plt.subplot(3, 2, j)
    plt.subplots_abjust(hspace=0.4)
    plot_desision_regions(X=X_combined_sepal, y=y_combined_sepal, classifier=lr,test_idx=range(0, 150))
    plt.xlabel('Sepal length')
    plt.ylabel('Sepal width')
    plt.title('C=%s'%i)

如果C值为10重做逻辑回归：

1
2
3
4
5
6
lr = LogisticRegression(penalty='l2', C=10)
lr.fit(X_train_sepal, y_train_sepal) # 训练机器
score = lr.score(X_test_sepal, y_test_sepal) # 测试集分数评估
print("SKlearn逻辑回归测试准确率{:.2f}".format(score*100))

# SKlearn逻辑回归测试准确率80.00

课后练习

一 根据这一节的练习案例数据集，泰坦尼克数据集（见源码包），并使用本节的方法完成逻辑回归。

二 在多元分类中，我们基于鸢尾花特征，进行了多元分类，请用类似的方法进行花瓣特征集的分类。

三 基于花瓣特征集，进行正则化参数C值的调试。