深度神经网络——找出可能流失的客户

这次的实战，是有关于一个金融领域的项目，而它需要神经网络，也就是深度学习模型来解决。深度学习是一个进阶领域，涉及到的新内容较多，因此此节内容会比较长，我会分成几个博客来写。
该项目的具体需求是根据已知的一批客户数据，来预测某个银行的客户是否会流失。通过学习历史数据，如果机器能够判断出哪些客户很有可能在未来两年内结束在该银行的业务，那么银行的工作人员就可以采用相应的措施来挽留这些高流失风险的客户。
其实这个问题和上一节的心脏病预测问题一样，本质上都是分类，而我们需要研究的就是，神经网络解决这一问题有什么优势。
本节用到的数据集在第5课源码包“教学用例 银行客户流失”目录中的“Bank Customer.csv”。

神经网络原理

传统机器算法的局限性

传统机器算法拥有一定局限性。首先，越简单的关系越容易拟合。然而对于一个非线性的问题，我们就需要通过复杂的函数模型（如高阶多项式）去拟合。此时单纯的线性回归函数已经不能满足要求，因而我们需要把特征重新组合，变化出新的特征。这种对特征的变换、升阶，以及多个特征相互组合形成新特征的过程，就是机器学习过程中即耗时又耗力的特征工程的一个例子。当特征的维度越来越大时，特征之间相互组合的可能性将以几何级数递增，特征空间急剧膨胀，对应的假设空间也随之膨胀，此时简单的模型已经不够看了。
计算机对于**非结构化数据（感知类数据）**不够敏感，例如图片、音乐等，因此对于它们的处理，计算机就不能使用简单的线性回归或者逻辑回归了。（你想，计算机看一张长宽为50像素的图片，就有2500个特征了哦！）
而神经网络就是专门为了解决这里超高特征维度的感知类问题诞生的。

神经网络的优势

神经网络实际上就像一张规模巨大的铁道网路，一头是上车的乘客，一头是乘客要到的站点，根据车票（特征），我们要让乘客正确到站（标签），这之间要经过重重的过渡站点，每次都要判定一下乘客的类别。如果第一次送错了，我们就要检查网路中的权重，让犯错的权重受到惩罚，而给判断正确的权重给予奖励。
书中用了一个分类猫图片还是狗图片的例子，相当生动，建议阅读书中原文。
因此精炼语言总结一下神经网络的机理：它是用一串一串的函数，也就是层，堆叠起来，作用于输入数据，进行从原始数据到分类结果的过滤于提纯。这些层通过权重来参数化，通过损失函数来判断当前网络的效能，然后通过优化器来调整权重，寻找从输入到输出的最佳函数。 注意以下两点：

  • 学习：就是为神经网络的每个层中的每个神经元寻找最佳的权重。
  • 知识：就是学到的权重。

从感知器到单隐层网络

神经网络由神经元组成，最简单的神经网络只有一个神经元，叫感知器。

感知器是最基本的神经元

下图代表一个神经元，它可以接受输入，并根据输入提供一个输出。

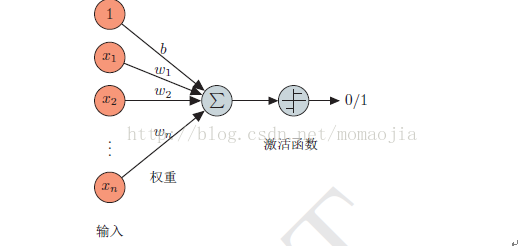
我们把图简单调整一下，左边的特征为(x0=b=1, x1, x2)，权重为(w0=-30, w1=20, w2=20)，激活函数为sigmoid，此时这个神经元变成了什么呢？它是一个与门！
看表：

x1 x2 z(x) g(z(x)) 逻辑值
0 0 -30 0.00001 0
0 1 -10 0.00001 0
1 0 -10 0.00001 0
1 1 40 0.99999 1

这就是最简单的一个逻辑回归的拟合，拟合函数是z(x)=20x1+20x2−30z(x)=20x_1+20x_2-30

它还能变成一个或门哦！只要把权重变成(w0=-10, w1=20, w2=20)
看表：

x1 x2 z(x) g(z(x)) 逻辑值
0 0 -10 0.00001 0
0 1 10 0.99999 1
1 0 10 0.99999 1
1 1 20 0.99999 1
拟合函数变成了z(x)=20x1+20x2−10z(x)=20x_1+20x_2-10

假设空间要覆盖特征空间

单神经元，通过训练可以用作逻辑回归分类器，那么它是如何进化成更复杂的多层神经网络呢？
我们需要重温几个概念。

  • 输入空间： x，输入值的集合。
  • 输出空间： y，输出值的集合。通常，输出空间会小于输入空间
  • 特征空间：每一个样本被称作一个实例，通常由特征向量表示，所有特征向量存在的空间称为特征空间。特征空间有时候于输入空间相同，有时候不同。有时候经过特征工程之后，输入空间可通过某种映射生成新的特征空间。
  • 假设空间： 假设空间一般是对于学习到的模型（即函数）而言的。模型表达了输入到输出的一种映射集合。假设空间代表着模型学习过程中能够覆盖的最大范围

单神经元特征空间的局限性

上节提到的感知器可以成功拟合“与门”和“或门”，但是却拟合不了“同或门”或者“异或门”。
比如举一个“同或门”的例子：

x1 x2 逻辑值
0 0 1
0 1 0
1 0 0
1 1 1

无论你怎么调整函数权重，都无法做到这个事情。其实我们可以用初中的线性规划知识证明这一点！
想一想，在一个平面直角坐标系中，你要画一条线，让点（1，1）和（0，0）在直线上方，并且（1，0）和（0，1）在直线下方，你会发现，你画不出这一条线。我们来代数推算一下：
直线方程：w1x1+w2x2+b=0w_1x_1+w_2x_2+b=0
目标：找到合适的w1,w2w_1,w_2
满足：{w1+w2+b>0b>0w1+b<0w2+b<0\begin{cases} w1+w2+b>0 \\ b>0\\ w1+b<0 \\ w2+b<0 \\ \end{cases}
将上两式相加，和下两式相加，你会发现矛盾：
{w1+w2+2b>0w1+w2+2b<0\begin{cases} w1+w2+2b>0 \\ w1+w2+2b<0 \\ \end{cases}

因此，我们需要增加网络的层数解决这个问题，其实，再增加一层网络，就相当于我们在线性规划的时候，多了一条可以使用的直线。