用keras单隐层网络预测客户流失率

这一节的实例过程中出现的结果，每个人之间可能都有较大出入。大家主要还是要理解代码的思路！另外下载教学资源中，此节的数据集和kaggle上作者上传的数据有所差别，强烈建议下载kaggle上的数据集：点击此处

数据准备与分析

打开数据集观察一下，会发现具体包含以下信息：

  • Name: 客户姓名
  • Gender: 性别
  • Age: 年龄
  • City: 城市
  • Tenure: 已经成为客户的年头
  • ProductsNo: 拥有的产品数量
  • HasCard: 是否有信用卡
  • ActiveMember: 是否为活跃用户
  • Credit: 信用评级
  • AccountBal: 银行存款余额
  • Salary: 薪水
  • Exited: 客户是否已经流失
1
2
3
4
import numpy as np
import pandas as pd
df_bank = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/Learning ML from 0/dataset/BankCustomer.csv")
df_bank.head()

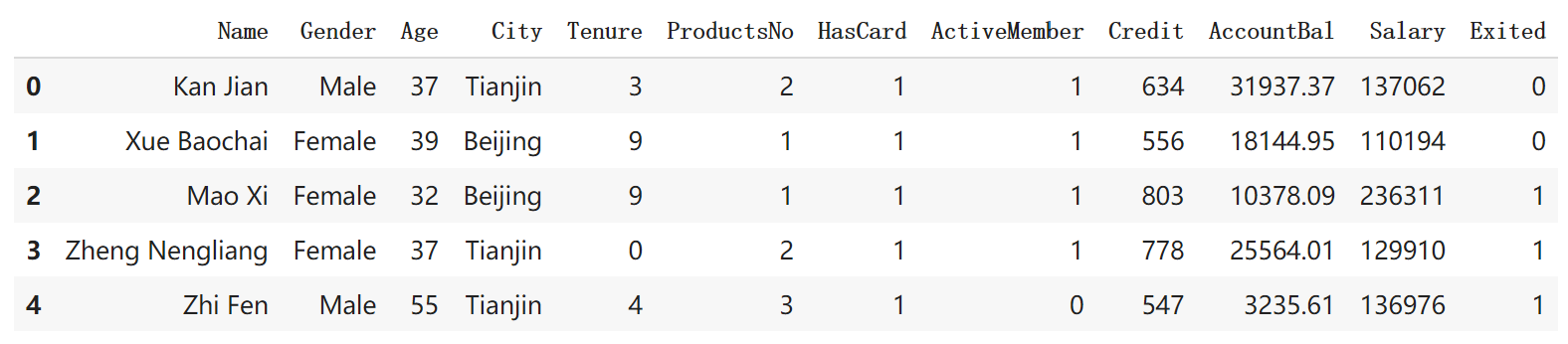
显示一下数据的分布情况：

1
2
3
4
5
6
7
8
9
10
import matplotlib.pyplot as plt
import seaborn as sns
# 显示不同特征的分布情况
features = ['City', 'Gender', 'Age', 'Tenure', 'ProductsNo', 'HasCard', 'ActiveMember', 'Exited']
fig = plt.subplots(figsize=(15, 15))
for i, j in enumerate(features):
    plt.subplot(4, 2, i+1)
    plt.subplots_adjust(hspace=1.0)
    sns.countplot(x=j, data=df_bank)
    plt.title('No. of costumers')

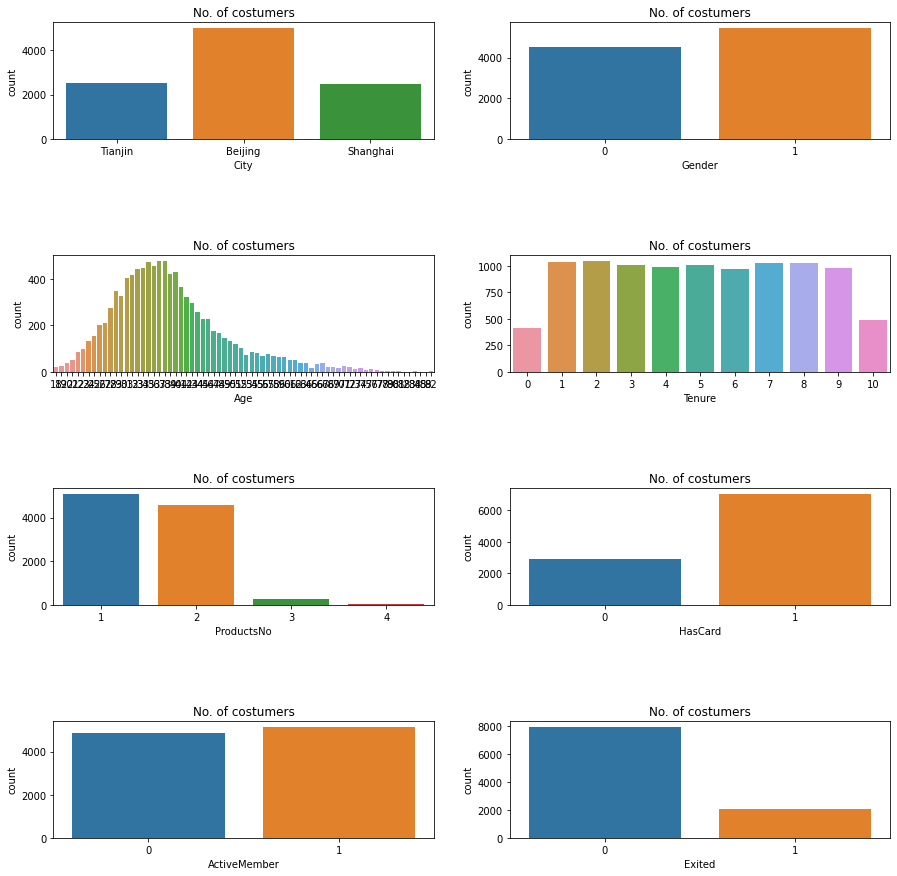
从图中看出，北京客户最多，男女比例基本一致，年龄和客户呈正态分布。对这个数据集需要做以下几个方面的清理工作：

  • （1）性别。这是一个二元类别特征，需要转化成1和0。
  • （2）城市。这是一个多元类别特征，应该转换成多个二元类别哑变量。
  • （3）姓名这个字段和客户流失与否无关，可以忽略。
1
2
3
4
5
6
7
8
9
10
11
12
13
# 把二元类别文本数字化
df_bank['Gender'].replace("Female", 0, inplace=True)
df_bank['Gender'].replace("Male", 1, inplace=True)
# 显示数字类别
print("Gender unique values", df_bank['Gender'].unique())
# 把多元类别转换成多个二元类别哑变量，然后放回原始数据集
d_city = pd.get_dummies(df_bank['City'], prefix='City')
df_bank = [df_bank, d_city]
df_bank = pd.concat(df_bank, axis=1)
# 构建标签和特征集
y = df_bank['Exited']
X = df_bank.drop(['Name', 'Exited', 'City'], axis=1)
X.head()

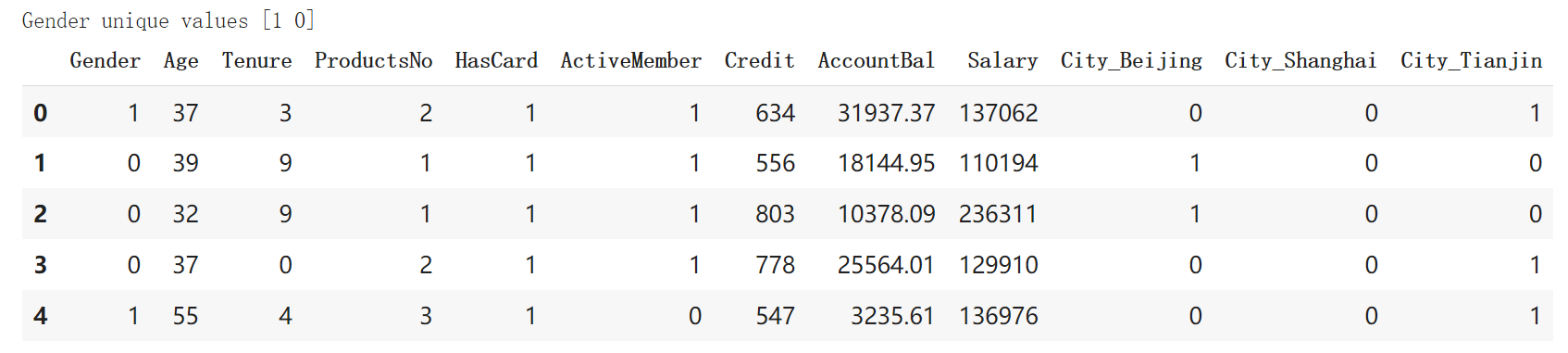
输出的清理之后的数据集如下图所示。此时新数据集的特征数目是12个。

1
2
3
4
5
6
7
8
9
10
11
# 拆分数据集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 尝试使用逻辑回归算法
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
history = lr.fit(X_train, y_train) # 训练机器
print("逻辑回归预测准确率{:.2f}%".format(lr.score(X_test, y_test)*100))

# 逻辑回归预测准确率78.35%

上面的结果是用上节的逻辑回归做的。下面我们尝试使用神经网络算法，准确率会不会提高。

单隐层网络的keras实现

1.用序贯模型构建网络

1
2
3
import keras
from keras.models import Sequential # 导入序贯模型
from keras.layers import Dense # 导入全连接层
  • 序贯模型，也可以叫做顺序模型，是最常用的深度网络层和层间的架构，也就是一个层接着一个层顺序堆叠。
  • 密集（dense）层，是最常用的深度网路层的类型，也称全连接层，即当前层和下一层的所有神经元都连接。

搭建网络模型：

1
2
3
4
5
ann = Sequential()
ann.add(Dense(units=12, input_dim=12, activation='relu')) # 添加输入层
ann.add(Dense(units=24, activation='relu')) # 添加隐层
ann.add(Dense(units=1, activation='sigmoid')) # 添加输出层
ann.summary() # 显示网络模型（此语句非必要，只用作显示）

summary方法显示了神经网络的结构，包括每个层的类型、输出张量的形状、参数数量以及整个网络的参数数量。上面这个网络有3层，493个参数（就是每个神经元的权重等），这对于神经网络来说，参数数量已经是比较少了。

通过下面的代码还可以展示出神经网络的形状结构：

1
2
3
4
from IPython.display import SVG # 实现神经网络结构的图形化显示
from keras.utils.vis_utils impo
rt model_to_dot
SVG(model_to_dot(ann, show_shapes=True).create(prog='dot',format='svg'))

模型的创建：ann=Sequential()创建了一个序贯神经网络模型。在Keras中，绝大部分的神经网络都是通过序贯模型所创建的。另外还有一种模型，称为函数式API，可以创建更为复杂的网络结构。
输入层：通过add方法，可开始神经网络层的堆叠，序贯模型，也就是一层一层的顺序堆叠。

Dense是层的类型，代表密集层网络，是神经网络层中最基本的层，也叫全连接层。类似的还有CNN中的Conv2D层，RNN中的LSTM层，等等。
input_dim是输入维度，输入维度必须维度必须和特征维度相同。
unit是输出维度，设置为12，这个值是随意选择的，这代表了经过线性变化和激活之后的假设空间维度，也就是神经元的个数。维度越大，则模型的覆盖面也越大，但是模型就越复杂，需要的计算量就越多。
activation是激活函数，这是每一层都需要设置的参数。这里的激活函数选择的是"relu"，而不是Sigmoid.
隐层：仍然通过add方法。在输入层之后的所有层都不需要重新指定输入维度，因为网络能够通过上一层的输出自动地调整。这一层的类型同样是全连接层。
输出层：仍然是一个全连接层，指定的输出维度是1。因为对于二分类问题，输出维度必须是1.对于二分类问题的输出层，Sigmoid是固定的选择。 如果是用神经网络解决回归问题的话，那么输出层不用指定任何激活函数。

下面编译刚才建好的这个网络：

1
2
3
4
# 编译神经网络，指定优化器、损失函数，以及评估指标
ann.compile(optimizer='adam', # 优化器
loss='binary_crossentropy', # 损失函数
metric=['acc']) # 评估指标

用Sequential模型的complie方法对整个网络进行编译时，需要指定以下几个关键参数。

优化器（optimizer）：一般情况下，“adam”或者“rmsprop”都是很好的优化器选项，但也有其他可选的优化器。
损失函数（loss）：对于二分类问题来说，基本上二元交叉熵函数（bc）是固定选项；如果是用神经网络解决线性的回归问题，那么均方误差函数是合适的选择。
评估指标（metrics）：这里采用预测准确率acc（也就是accuracy的缩写，两者在代码中的是等价）作为评估网络性能的标准；而对于回归问题，平均误差函数是合适的选择。准确率，也就是正确地预测占全部数据的比重，是最为常用的分类评估指标。

2.全连接层

全连接层（Dense层）是最常见的神经网络层，用于处理最普通的机器学习向量数据集，即形状为（标签，样本）的2D张量数据集，其实现了一个逻辑回归功能：

Output=Activation(dot(input,kernel)+bias)Output = Activation(dot(input,kernel)+bias)

公式中的kernel，其实就是权重。网络是多节点的，所以它从向量升级为矩阵，把输入和权重矩阵做点积，然后加上一个属于该层的偏置，激活之后，就得到了全连接层往下一层的输出。偏置是可有可无的，不是必需项。
其实，每层最基本的、必须设置的参数只有以下两个。

  • units:输出维度。
  • activation:激活函数。

对于输入层，当然还要多指定一个输入维度。对于后面的隐层和输出层，则连输入维度也可以省略。

1
2
3
4
5
6
7
8
9
10
keras.layers.Dense(unit=12,
                activation=None,
                use_bias=True,
                kernel_initializer='glorot_uniform',
                bias_initializer='zeros',
                kernel_regularizer=None,
                bias_regularizer=None,
                activity_regularizer=None,
                kernel_constraint=None,
                bias_constraint=None)

3.其他层

常见的其他层还有：

  • 循环层（如Keras的LSTM层），用于处理保存在形状为（样本，时戳，标签）的3D张量中的序列数据。
  • 二维卷积层（如Keras的Conv2D层），用于处理保存在形状为（样本，帧数，图像高度，图像宽度，颜色深度）的4D张量中的图像数据。

训练单隐层神经网络

通过fit方法实现拟合过程：

1
2
3
4
history=ann.fit(X_train, y_train,
            epochs=30,
            batch_size=64,
            validation_data=(X_test, y_test))
  • batch_size：用于指定数据批量，也就是每一次梯度下降更新参数时所同时训练的样本数量。这是利用了CPU/GPU的并行计算功能，系统默认值是32。
  • validation_data：用于指定验证集。这样就可以一边用训练集网络，一边验证某评估网络的效果。为了简化模型，就直接使用测试集来验证。

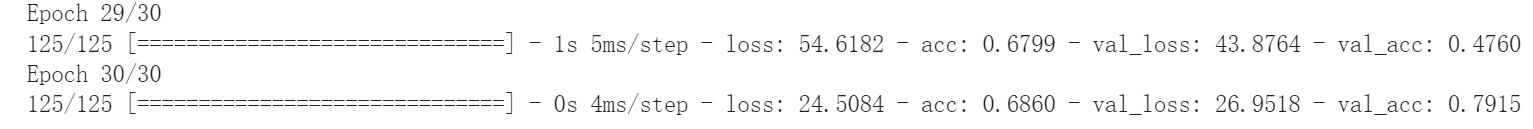
我这里最后的准确率是79.15%，还算不错，虽然我不太清楚这个数据是否具有可信度。

训练过程的图形化显示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def show_history(history):
  loss = history.history['loss']
  val_loss = history.history['val_loss']
  epochs = range(1, len(loss)+1)
  plt.figure(figsize=(12, 4))
  plt.subplot(1, 2, 1)
  plt.plot(epochs, loss, 'bo', label='Training loss')
  plt.plot(epochs, val_loss, 'b', label='Validatiion loss')
  plt.title('Training and validation loss')
  plt.xlabel('Epochs')
  plt.ylabel('Loss')
  plt.legend()
  acc = history.history['acc']
  val_acc = history.history['val_acc']
  plt.subplot(1, 2, 2)
  plt.plot(epochs, acc, 'bo', label='Training acc')
  plt.plot(epochs, val_acc, 'b', label='Validation acc')
  plt.title('Training and validation accuracy')
  plt.xlabel('Epochs')
  plt.ylabel('Accuracy')
  plt.legend()
  plt.show()

show_history(history)

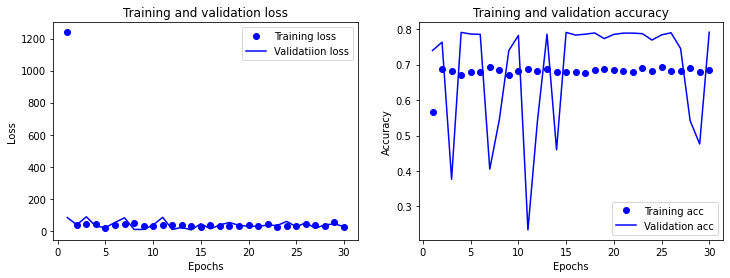
分类数据不平衡问题

看上去79.15%的准确率挺高的，还蛮不戳的，但实际上，这一次的预测结果是非常失败的。因为原本数据集中，10000个客户里面有大约8000个客户都是不会离开的，那我预测所有用户都不会离开，不也猜对了80%嘛，大差不差。那这情况是什么引起的呢？是因为数据集中标签类别数据非常不平衡，一方太多一少。 下面给出一个极端的例子来讲解。

例子

假设有一个手机厂商，每天生产1000台手机，有天1000台手机中出现了2台次品，现在需要通过机器学习来预测一个模型，可以展示该厂商的次品率。最后得到结果如下表：