matlab基础 工程篇(一 数值微积分)
前言
matlab是一款功能强大的计算工具。最近我重新学习了计算机视觉的相关知识,其中,使用matlab编写程式码是不可缺少的环节。然而在过程中我遗忘了许多的编写规则和内置函数,因此,为了重新掌握matlab语言,我试图寻找一些基础的课程或者教程。最终,我在B站上发现了一个讲解得极其优秀的课程,是由台湾大学教授郭彦甫主讲的《matlab教学》。
该课程共分14P,13节基础内容。涵盖初中级、高级、影像处理、工程相关四块内容。我在写这篇博客之前,已经将这些内容都学习完成,写文章的主要目的是回顾和总结学到的知识。而为了趁热打铁,博客开头将会从我最近学完的内容写起,即“工程相关”的一块。
在使用matlab之前,请确保拥有一些必要的高等数学、微积分、线性代数、概率统计知识。(不过别担心,稍微复杂的地方在课程中会有解释)
这里附上B站视频链接:MATLAB教程_台大郭彦甫(14课)原视频补档
最后我要再一次强烈安利一下这门课:台湾口音很可爱、课程内容不困难、老师讲解很细致,总之就是非非非常的nice!
下面让我们开始吧!
matlab与数值微积分
matlab与微积分的联系主要在关于两块内容:多项式微分、积分(polynomial differentiation and integration)和数值微分、积分(Numerical differentiation and integration)
多项式方面主要与多项式求导、积分的公式相关,数值方面主要与求导数定义方法有关。
matlab中的多项式微分
在微积分与高等数学中我们知道,多项式(polynomial)可表达为:
其导数形式为:
对于一个多项式,在matlab中我们只需要考虑用系数表达就可以,例如以下这个多项式:
我们可以提取系数写作一个向量复制给P:
1 | p = [3 0 1 -4] |
- 显然原式中没有二次项,或者说二次项系数等于0.
polyval()
在matlab中绘制一个多项式函数可以使用polyval的方法。
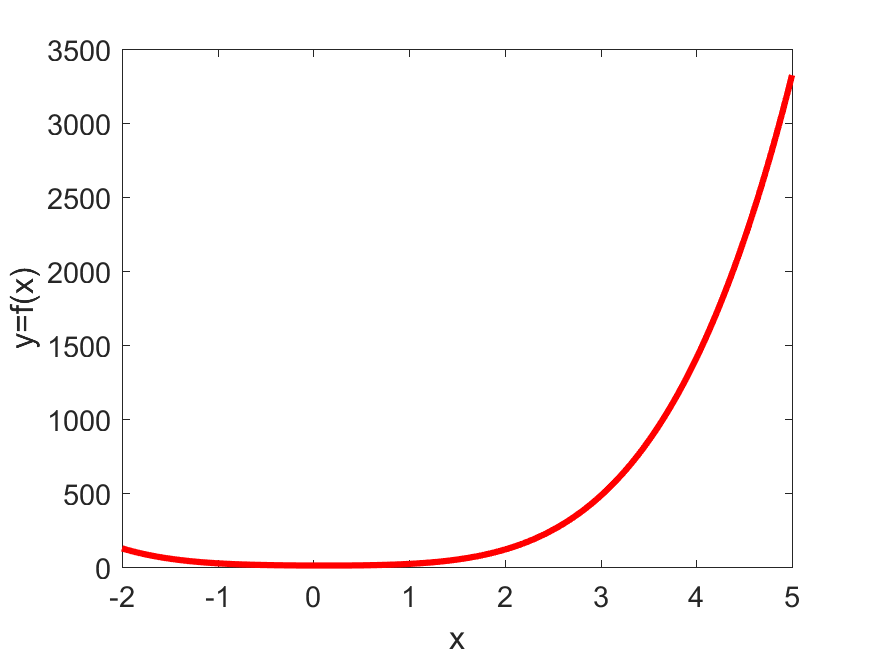
例,在定义域 绘制函数
我们可以在定义域上对函数进行采样,取许多点连成线即可。polyval方法实际上的工作就是,当x=a时,计算f(x)=f(a)的值。
1 | P=[5 0 8 -2 9]; x=-2:0.01:5; |
polyder()
在matlab中绘制一个多项式的导函数可以使用polyder方法。
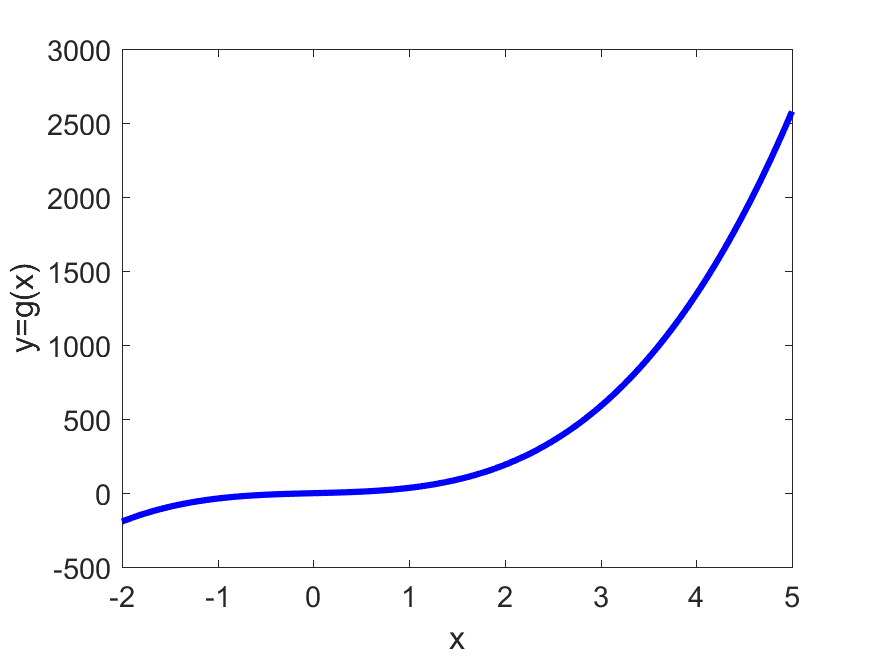
例,在定义域 绘制函数 的导函数。
polyder的作用就是返回该多项式函数的导函数的系数向量。
1 | P=[5 0 8 -2 9]; x=-2:0.01:5; |
例题:
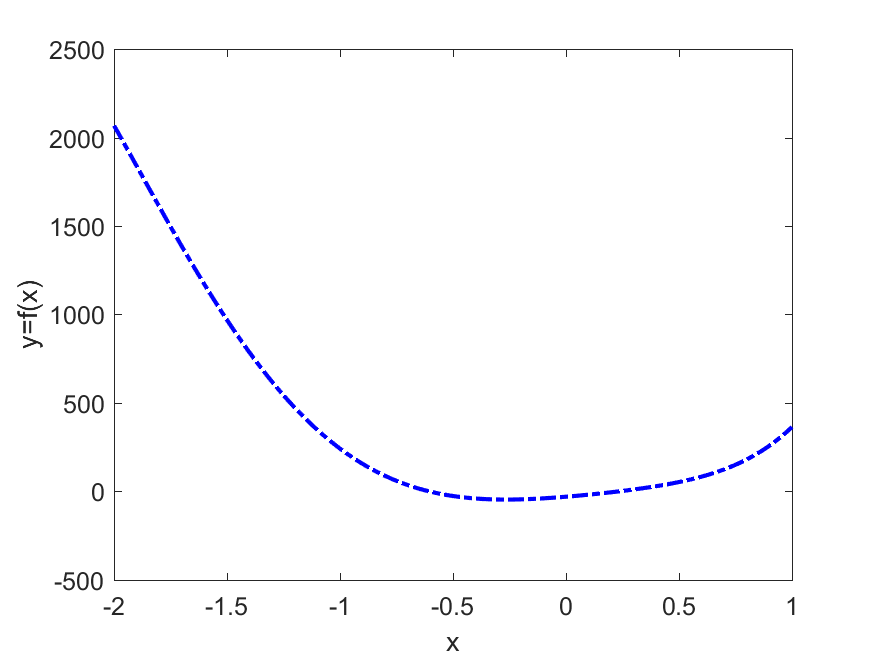
Plot the polynomial
and its derivative for $-2 \leq x \leq 1 $
Hint: Try to use function conv()
1 | a = [20 -7 5 10]; b = [4 12 -3]; |
matlab中的多项式积分
同样的多项式
其积分形式为:
polyint()
因为积分之后表达式多出了一个常数项C,C可以为任意值,这使得表达式不唯一了。所以在绘制时需要给定常数项具体值,polyint方法的第二个参数就是给定的常数。
例,在定义域 绘制函数 的积分函数,常数项
1 | P=[5 0 8 -2 9]; x=-2:0.01:5; |
matlab中的数值微分
显然,对于多项式的微分和积分我们有现成的公式可以套用,可对于sin(x),cos(x),ln(x)这种,虽然许多我们也有公式,但是太不统一了,我们需要有一种统一的方法去描述,所以我们可以从导数定义法入手。
这个表达式的右侧实际上是一个非常小的三角形(微分三角形)的tan值,可以近似于某一点的斜率。所以实际上,我们只要在原函数上采样,算一系列点的斜率,然后再绘制这一系列点,连起来即可,显然,这一系列点越近效果就越好。例如当差值为0.01,取x=0.01,0.02,0.03……
diff()
我们可以使用diff方法批量处理差值。diff返回的就是一个向量中间元素的差值,例如:
1 | v = [1 2 5 2 1]; |
- 注意方向,是后一个元素减去前一个元素。
应用到求斜率上呢?
1 | x = [1,2]; y=[3,4]; %已知两个点 |
再推广到函数导数上:
例如,要找y=sin(x)的当x=pi/2时的导数值,使用 = 0.1:
1 | x0 = pi/2; dx=0.1; |
再推广到整个区间上,例如当时,sin(x)的导函数,为精确一点,另dx=0.01
1 | dx = 0.01; |
- 注意,使用diff之后,差值构成的向量维度要比原数据构成的向量少1,所以要使用x(1:end-1),截去最后一个元素。
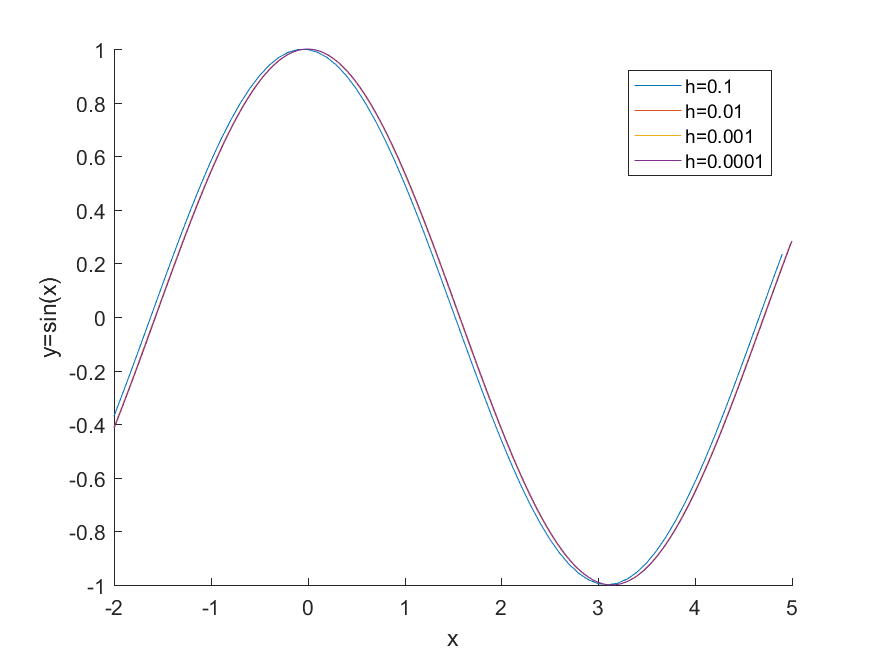
这里给出一个用不同精确度dx的例子,使dx分别等于0.1,0.01,0.001,0.0001,看看效果差多大。
1 | g = colormap(lines); |
二次导数和三次导数
二次导数实际上就是对diff求得的差值向量再做一次差值,三次导数类似。例如:
1 | x = -2:dx:5; y=sin(x); |
matlab中的数值积分
数值积分实际上可以看作求曲线与坐标X轴包围的面积。在之前我们已经在x轴上取出了一个一个的小范围,我们只需要用上这个结合函数划分一块一块小区域就行。不过区域也有不同的画法,主流的有三种方法(规则)。
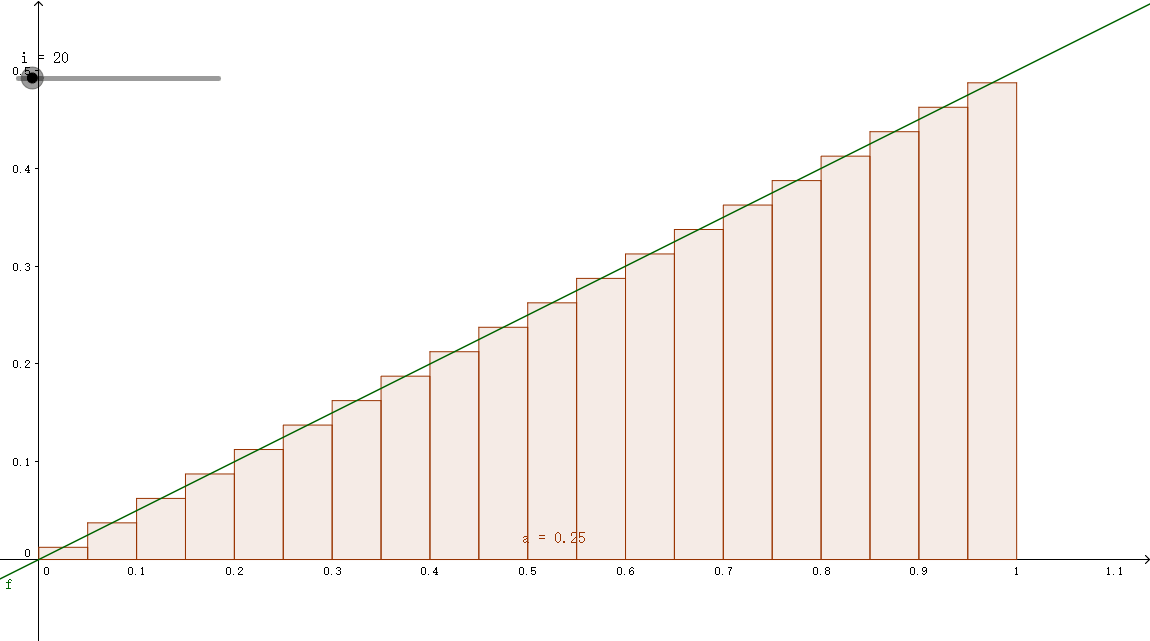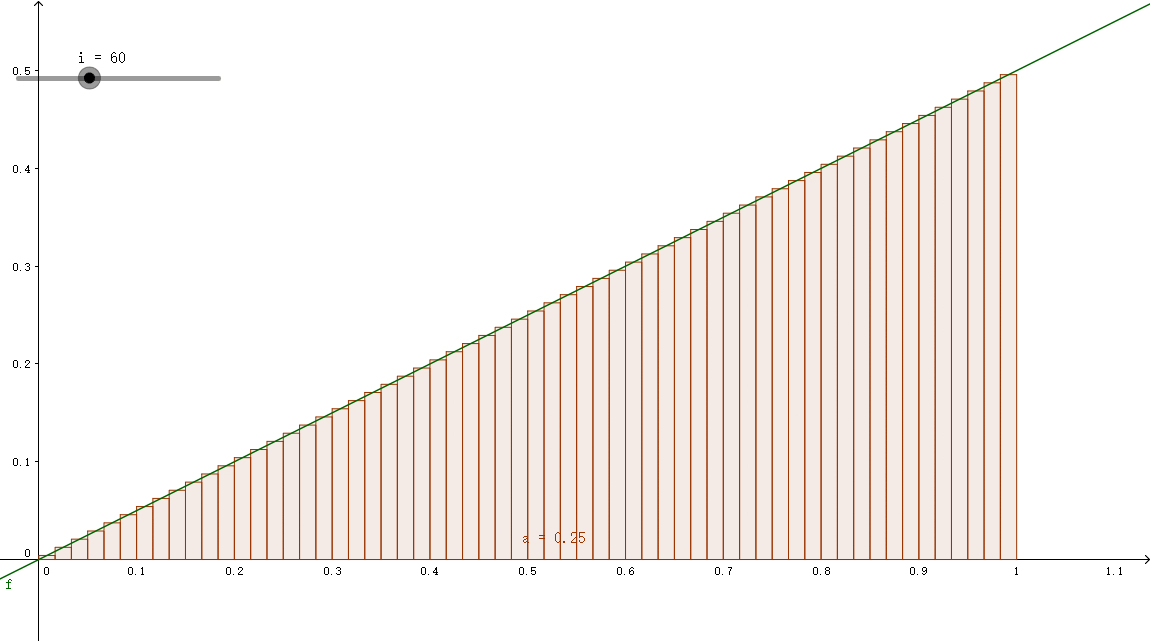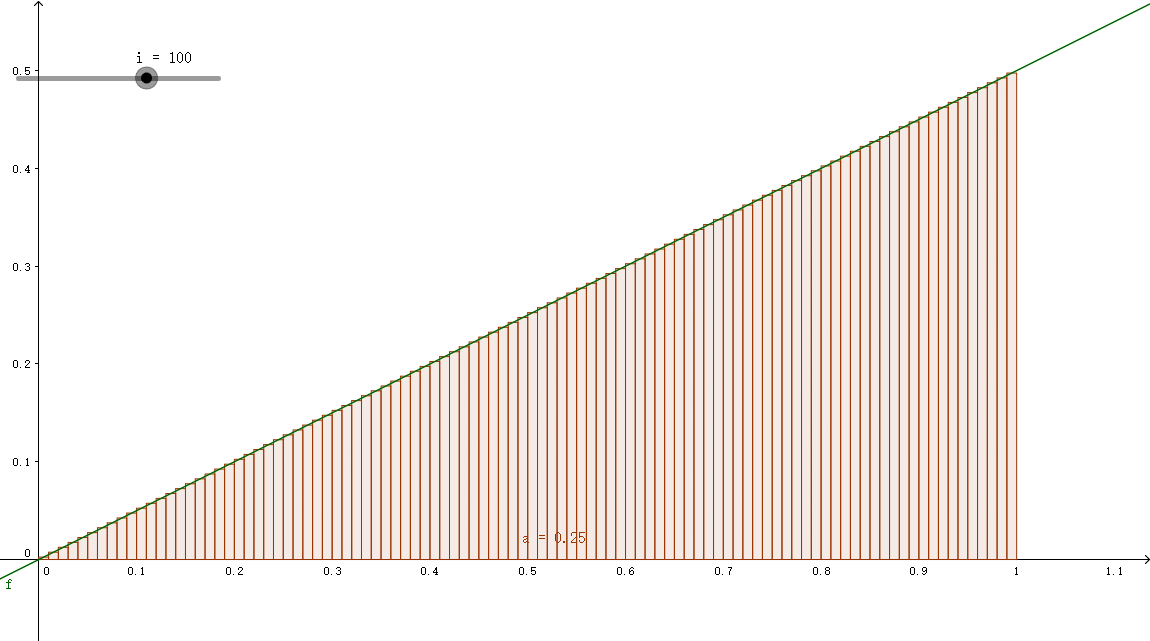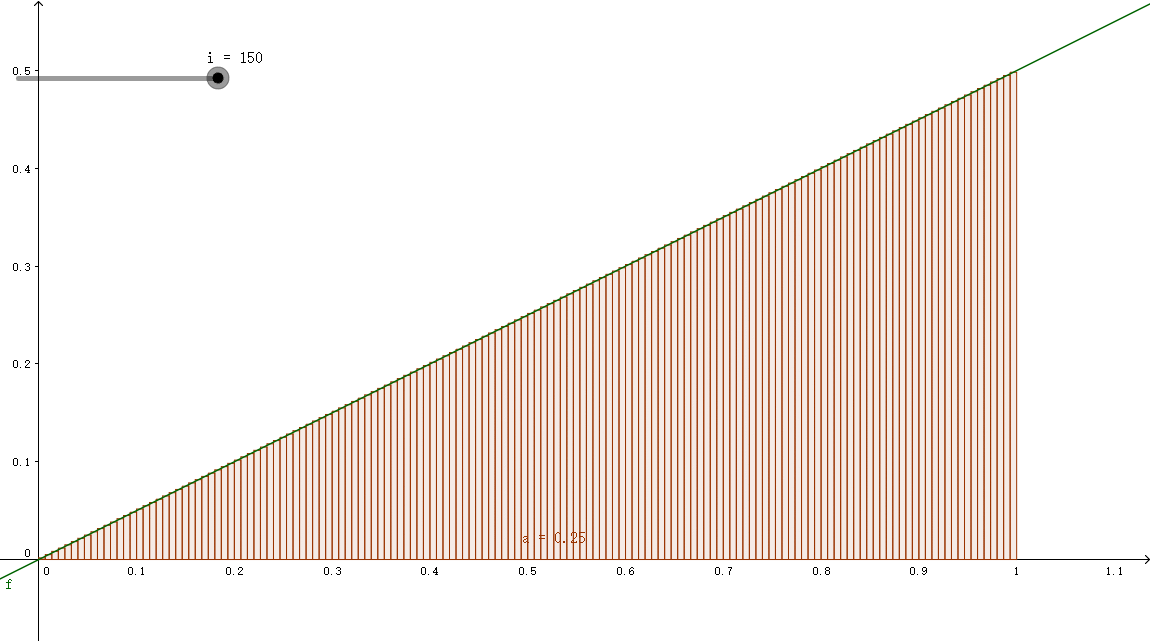
中点法则(midpoint rule)
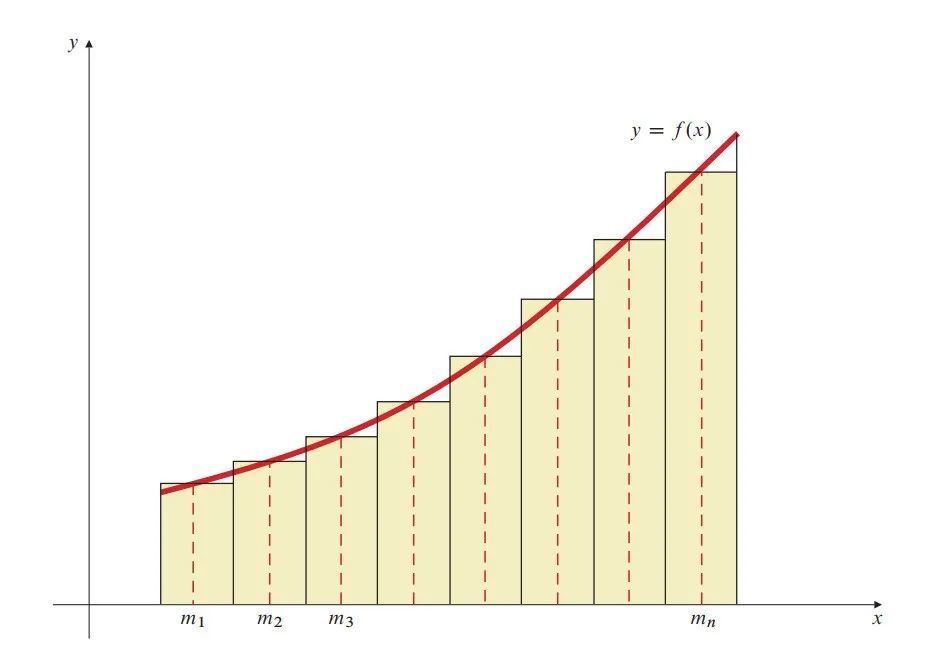
例如上图中最左侧的小长方形,其左侧为x0,右侧为x1,所以小矩形的面积为
例题: 计算在上的积分。dx设置为0.02.
1 | dx = 0.02; |
梯形法则(trapezoidal rule)
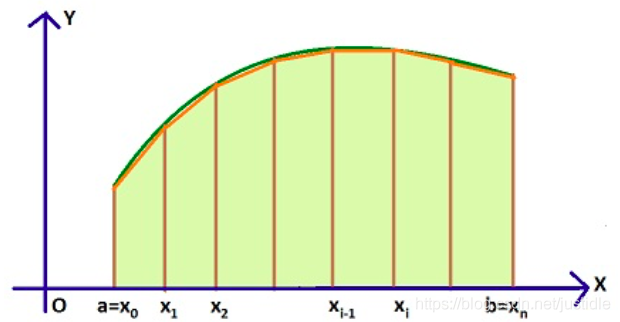
如上图,实际上就是用一个梯形取代了矩形,我们就不需要求中点了,每一块梯形用梯形面积公式就可以。
matlab为我们提供了梯形法则的函数trapz(),当然我们也可以自己算。
仍然用刚刚的例题:
1 | dx = 0.02; |
辛普森法则(Simpson rule)
辛普森法则又被叫做三分之一辛普森法则(1/3 Simpson rule)
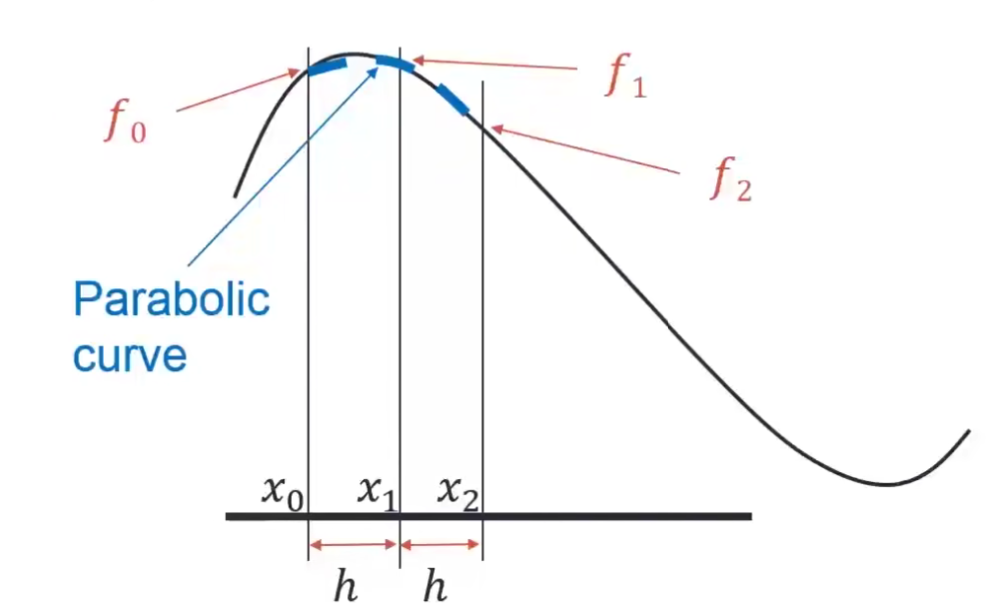
实际上他是结合了上述的两种方法,一次性算两块小区域,同时考虑三个点的影响。如果说矩形的上端可以看作零次函数(曲线),梯形的上端可以看作一次函数(曲线),那么辛普森法则的小区域可以被看作一个二次函数(曲线)。用越高次的曲线去贴近原函数,当然就更加精确咯!
具体的表达式是这样的:
同样的例题:
1 | dx = 0.02; |
补充方法
实际上matlab中为我们准备了内置的积分函数integral(),不过使用这个函数需要我们了解matlab的函数句柄(function handle)符号“@”。
function handle实际上就是一个函数的指针,例如C++中的回调函数等等,它允许我们可以在一个函数中调用另一个函数。
语法为: 变量名=@(输入参数列表)运算表达式
这样产生的函数句柄变量不指向特定的函数, 而是一个函数表达式。
例如:
1 | y = @(x) x.^2*log(x); |
另外,二重积分和三重积分分别可以使用integral2()和integral3()
1 | f = @(x,y) x.*cos(y)+y.*sin(x); |
此小节结束,你真厉害!