matlab中的回归与内插
简单线性回归(simple linear regression)
首先想象,在一个坐标系中存在着一些离散的点,现在我们需要用一条线去拟合这些点,这就是简单线性回归。使用一次函数拟合是最为简单的情况。
在平面中,存在i组点 ( x i , y i ) (x_i,y_i) ( x i , y i ) y i ^ = β 0 + β 1 x \hat{y_i}=\beta_0+\beta_1 x y i ^ = β 0 + β 1 x
最小二乘法(ordinary least squares)
最小二乘法简单理解为每个离散点到拟合直线的距离的平方和最小,不过这个距离不是点到直线的距离,而是y方向的差值,即 d i s i = y i − y ^ i dis_i=y_i-\hat y_i d i s i = y i − y ^ i
首先,根据最小二乘法的原理,我们可以写出距离平方和(sum of squared errors, SSE):
S S E = ∑ i d i s i 2 = ∑ i ( y i − y ^ i ) 2 SSE=\sum_i dis_i^2=\sum_i(y_i-\hat y_i)^2
SSE = i ∑ d i s i 2 = i ∑ ( y i − y ^ i ) 2
y ^ i = β 0 + β 1 x i \hat y_i =\beta_0+\beta_1 x_i
y ^ i = β 0 + β 1 x i
∑ i d i s i 2 = ∑ i ( y i − β 0 − β 1 x i ) 2 \sum_i dis_i^2=\sum_i(y_i-\beta_0-\beta_1 x_i)^2
i ∑ d i s i 2 = i ∑ ( y i − β 0 − β 1 x i ) 2
现在我们要使SSE最小,则需要求偏导。
∂ ∑ i d i s i 2 ∂ β 0 = − 2 ∑ i ( y i − β 0 − β 1 x i ) = 0 \frac{\partial \sum_i dis_i^2}{\partial \beta_0} = -2\sum_i(y_i-\beta_0-\beta_1 x_i)=0
∂ β 0 ∂ ∑ i d i s i 2 = − 2 i ∑ ( y i − β 0 − β 1 x i ) = 0
∂ ∑ i d i s i 2 ∂ β 1 = − 2 ∑ i ( y i − β 0 − β 1 x i ) x i = 0 \frac{\partial \sum_i dis_i^2}{\partial \beta_1} = -2\sum_i(y_i-\beta_0-\beta_1 x_i)x_i=0
∂ β 1 ∂ ∑ i d i s i 2 = − 2 i ∑ ( y i − β 0 − β 1 x i ) x i = 0
整理式子得:
∑ i = 1 N y i = β 0 N + β 1 ∑ i = 1 N x i \sum_{i=1}^N y_i=\beta_0 N+\beta_1 \sum_{i=1}^N x_i
i = 1 ∑ N y i = β 0 N + β 1 i = 1 ∑ N x i
∑ i = 1 N y i x i = β 0 ∑ i = 1 N x i + β 1 ∑ i = 1 N x i 2 \sum_{i=1}^N y_ix_i=\beta_0 \sum_{i=1}^N x_i+\beta_1 \sum_{i=1}^N x_i^2
i = 1 ∑ N y i x i = β 0 i = 1 ∑ N x i + β 1 i = 1 ∑ N x i 2
写成矩阵形式:
[ ∑ y i ∑ y i x i ] = [ N ∑ x i ∑ x i ∑ x i 2 ] [ β 0 β 1 ] \begin{bmatrix}
\sum y_i \\
\sum y_ix_i
\end{bmatrix}=
\begin{bmatrix}
N & \sum x_i \\
\sum x_i & \sum x_i^2
\end{bmatrix}
\begin{bmatrix}
\beta_0 \\
\beta_1
\end{bmatrix}
[ ∑ y i ∑ y i x i ] = [ N ∑ x i ∑ x i ∑ x i 2 ] [ β 0 β 1 ]
由此,我们可以解出 β 0 和 β 1 \beta_0 和\beta_1 β 0 和 β 1
那么如果不是一次函数,按照同样的方法也可以解出对应的需要的参数。
polyfit()
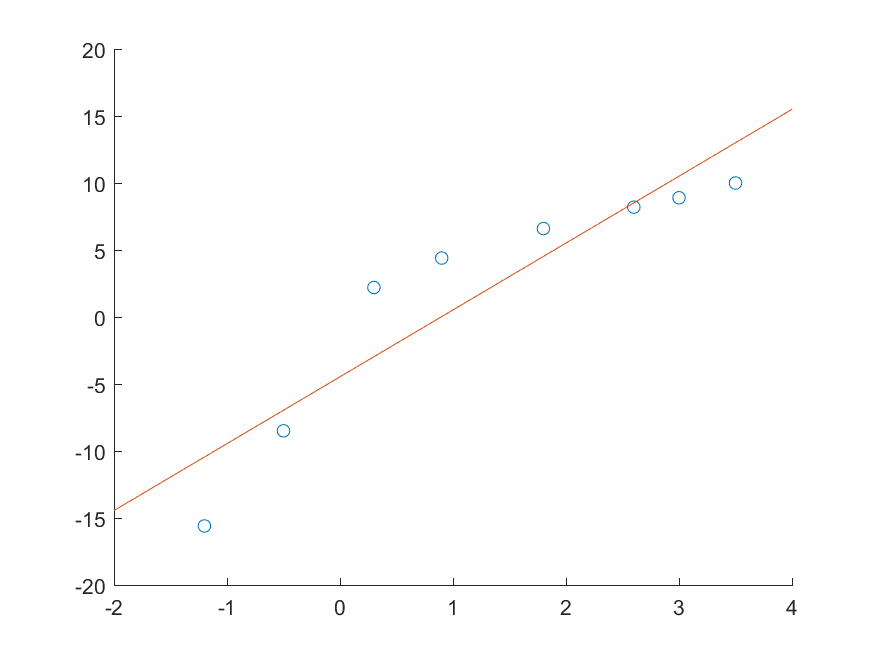
在matlab中,我们只需要提供点序列x的向量和y的向量,再使用polyfit函数就可以很快的拟合出需要的线了。
1 2 3 4 5 6 7 8 9 10 11 12 x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5 ]; y = [-15.6 -8.5 2.2 4.4 6.6 8.2 8.9 10.0 ]; fit=polyfit(x, y, 1 ) x1=-2 :0.1 :4 y1=polyval(fit, x1) figure hold onplot (x,y,'o' );plot (x1,y1)hold off
corrcoef()
corrcoef函数用来判定这些散点是否有线性相关(Linearly correlated),返回值为一个大于-1小于1的常数k,如果k接近-1,则说明这些点呈负相关,如果k接近1,则说明它们正相关,如果接近0,则说明它们线性无关。
1 2 3 x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5 ]; y = [-15.6 -8.5 2.2 4.4 6.6 8.2 8.9 10.0 ]; corrcoef(x,y)
corrcoef(x,y)返回的是一个二阶矩阵,左上角表示x和x的相关,右下角表示y和y的相关,所以肯定都是1,右上角和左下角表示的是x和y的相关以及y和x的相关。
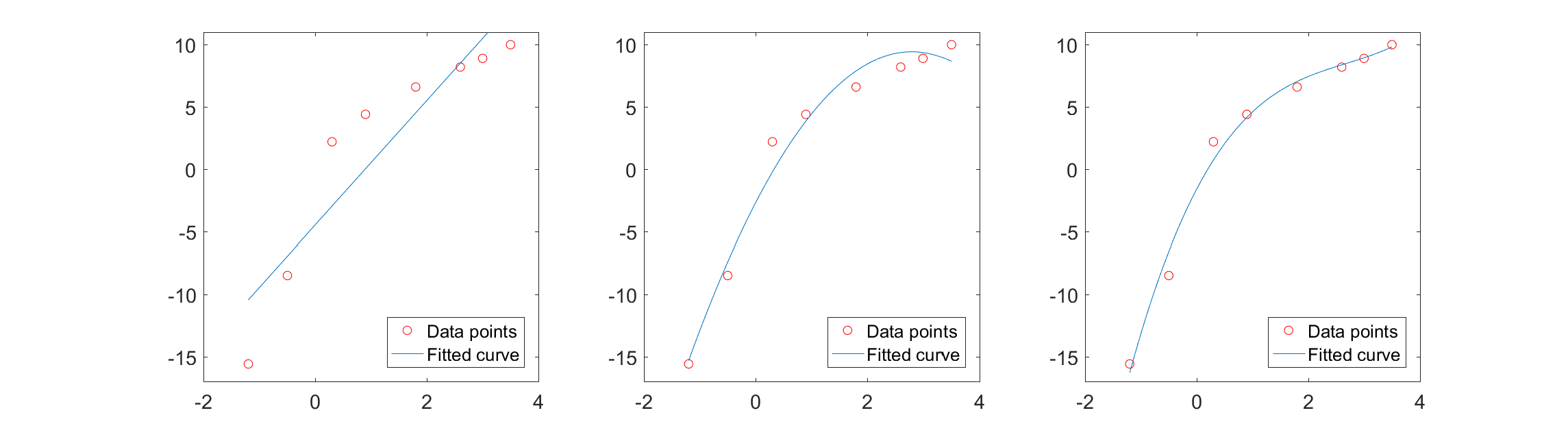
用更高次的函数拟合,有时候效果会更好,但也有可能过拟合。
1 2 3 4 5 6 7 8 9 10 11 x=[-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5 ]; y = [-15.6 -8.5 2.2 4.4 6.6 8.2 8.9 10.0 ]; x1=x(1 ):0.1 :x(end ); set(gcf, 'position' , [100 100 1500 400 ]); for i =1 :3 subplot(1 , 3 , i ); fit = polyfit(x, y, i ); y1=polyval(fit, x1); plot (x, y, 'ro' , x1, y1); set(gca, 'fontsize' , 14 ); ylim([-17 11 ]); legend ('location' , 'southeast' , 'Data points' , 'Fitted curve' ); end
regress()
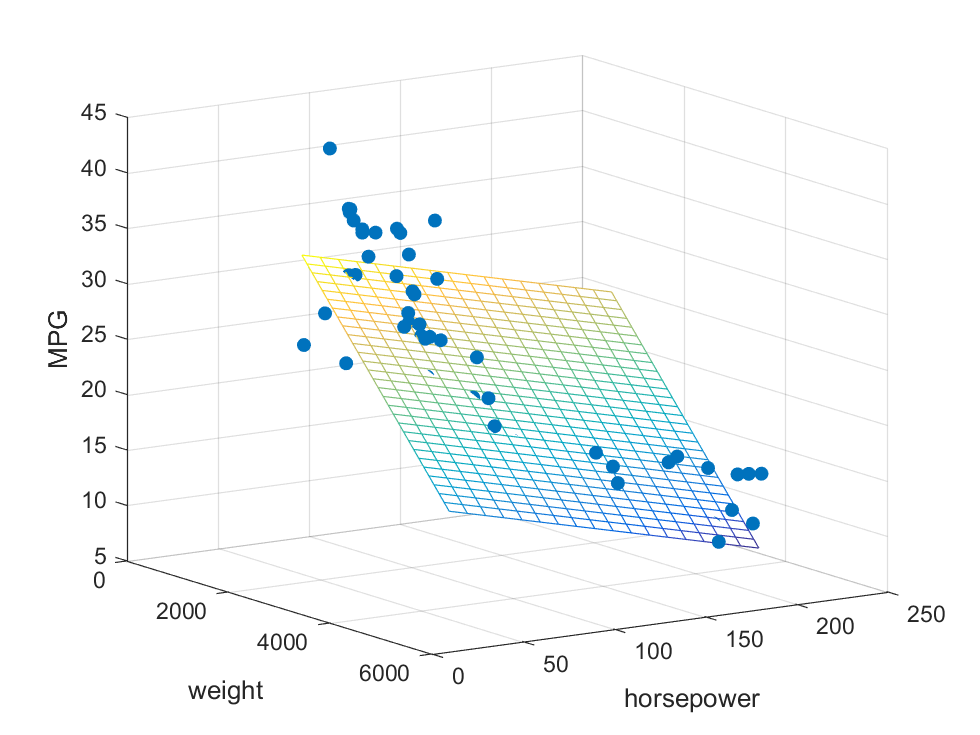
上面提到的polyfit仅适合拟合一元函数,如果我们要拟合多元函数怎么办?这时候就要用到regress().
先看一个matlab中内置的实例:
1 2 3 4 5 6 7 8 9 10 11 12 13 load carsmall; y = MPG; x1=Weight; x2=Horsepower; X = [ones (length (x1), 1 ), x1, x2]; b=regress(y, X); x1fit=min (x1):100 :max (x1); x2fit=min (x2):10 :max (x2); [X1FIT, X2FIT]=meshgrid (x1fit, x2fit); YFIT=b(1 )+b(2 )*X1FIT+b(3 )*X2FIT; scatter3 (x1,x2,y, 'filled' ); hold onmesh(X1FIT,X2FIT,YFIT); hold off xlabel('weight' ); ylabel('horsepower' ); zlabel('MPG' ); rotate3d on;
我们首先要按照 y = a + b x + c x 2 y=a+bx+cx^2 y = a + b x + c x 2
内插(interpolation)
内插的概念比较简单,主要看matlab中怎么应用吧。
interp1()
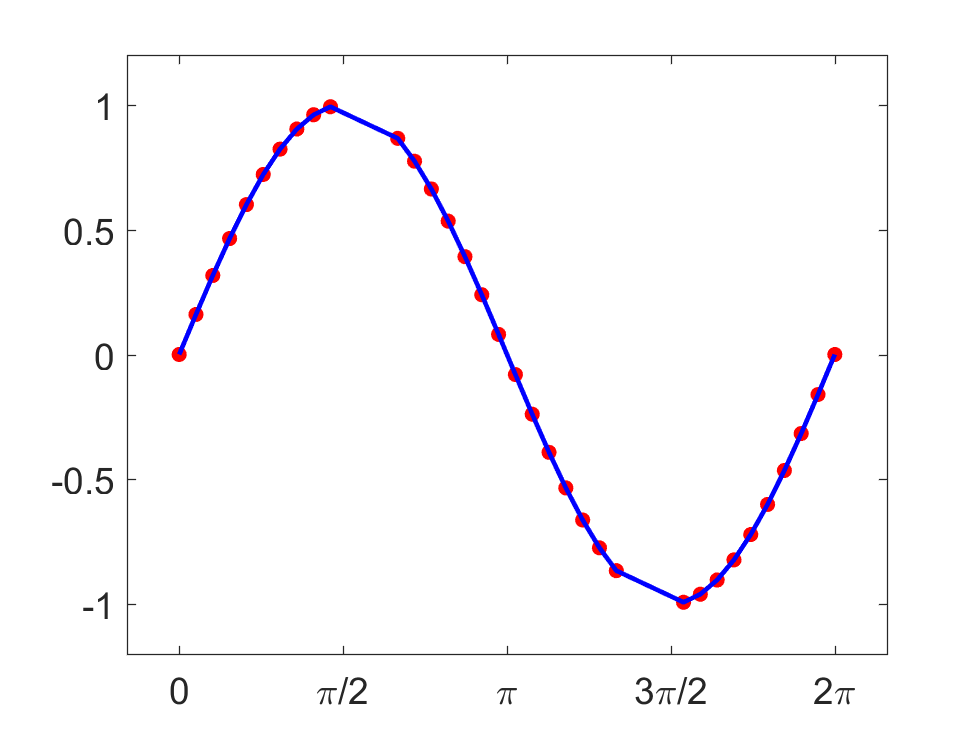
1 2 3 4 5 6 7 8 9 10 11 12 13 14 x=linspace (0 , 2 *pi , 40 ); x_m=x; x_m([11 :13 , 28 :30 ])=NaN; y_m=sin (x_m); plot (x_m, y_m, 'ro' , 'markerfacecolor' , 'r' );xlim([-0.5 2 *pi +0.5 ]); ylim([-1.2 1.2 ]); box on; set(gca, 'fontsize' , 16 ); set(gca, 'xtick' , 0 :pi /2 :2 *pi ); set(gca, 'xticklabel' , {'0' , '\pi/2' , '\pi' , '3\pi/2' , '2\pi' }); m_i=~isnan (x_m); y_i =interp1(x_m(m_i), y_m(m_i), x); hold onplot (x, y_i, '-b' , 'linewidth' , 2 );hold off
spline()
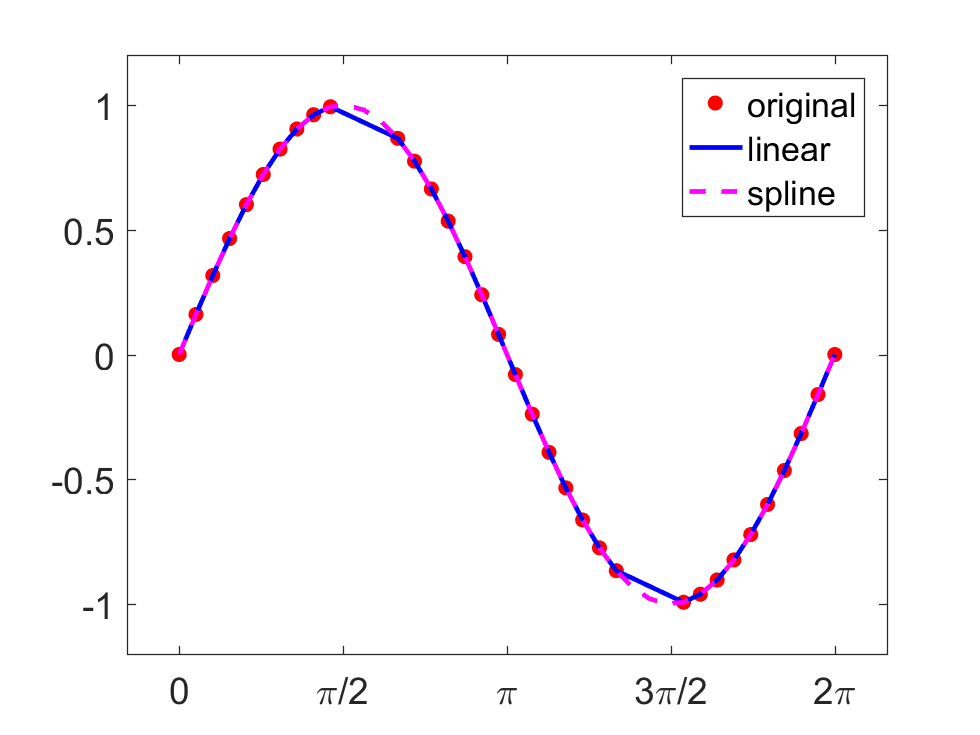
如果要让内插变得光滑,那么可以使用spline方法。只需要把interp1改成spline.
1 2 3 4 5 6 7 m_i=~isnan (x_m); y_i=interp1(x_m(m_i), y_m(m_i), x); y_s=spline(x_m(m_i), y_m(m_i), x); hold onplot (x, y_i, '-b' , x, y_s, '--m' , 'linewidth' , 2 );hold offh=legend ('original' , 'linear' , 'spline' );
pchip()
pchip是一种分段三次差值法,其原理来自于埃尔米特插值法
既然我们能做到不光滑和光滑的差值了,还要别的方法干嘛,先来看一个实例:
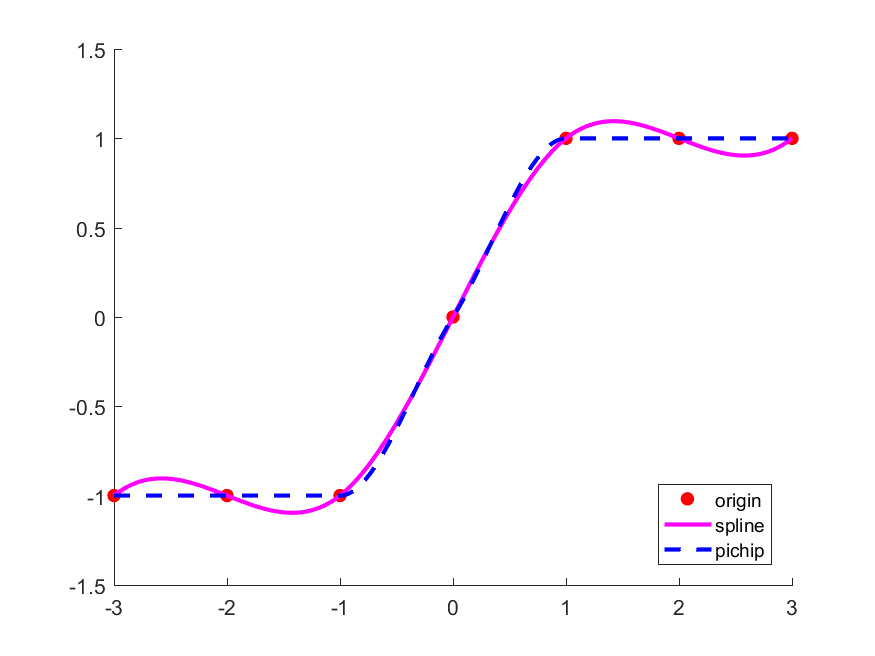
1 2 3 4 5 6 7 8 9 x = -3 :3 ; y = [-1 -1 -1 0 1 1 1 ]; t=-3 :0.01 :3 ; y_s = spline(x, y, t); y_p = pchip(x, y, t); hold onplot (x, y, 'ro' , 'markerfacecolor' , 'r' );plot (t, y_s, 'm-' , 'linewidth' , 2 );plot (t, y_p, 'b--' , 'linewidth' , 2 );hold offlegend ('location' , 'southeast' , 'origin' , 'spline' , 'pichip' );
不难发现,在这一个例子中,使用spline方法会让两边差值的形状产生波动,这就是龙格效应(rouge phenomenon) ——有些函数在差值的时候,差值次数越高,边缘区域就越不准确,波动越大。至于龙格效应出现的原理,我也还没弄明白,在这里插个眼,以后明白了会补充说明。
那么使用pchip方法就可以有效避免这个问题,因为埃尔米特插值法的一大优势就是为了解决龙格效应 ,至于怎么就解决了,我也没弄明白,啊哈哈哈哈(尴尬又不失礼貌的笑容)。
interp2()
当然,对于二维平面,matlab同样可以内插。
下面看一个实例,用法与以为相差不多。
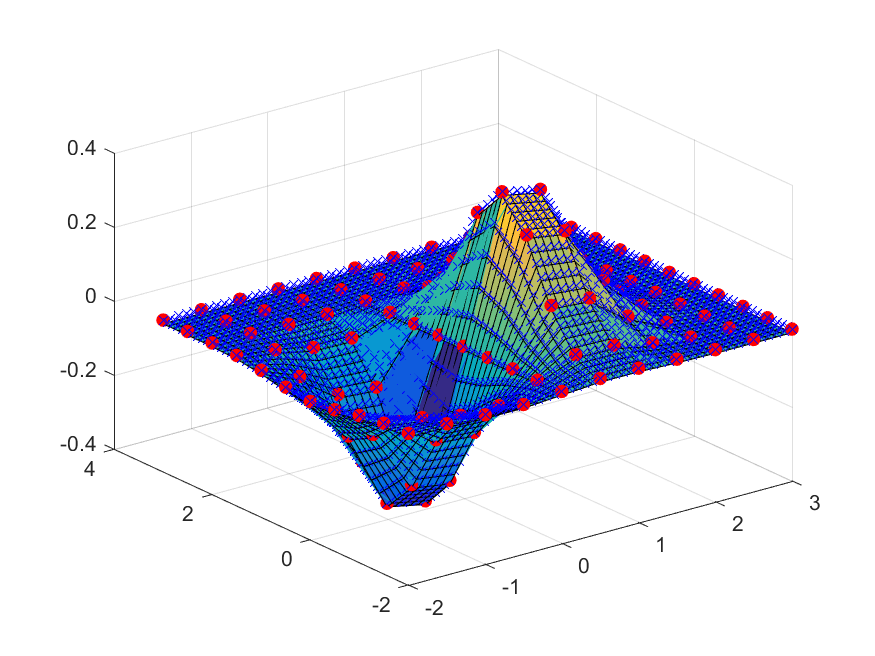
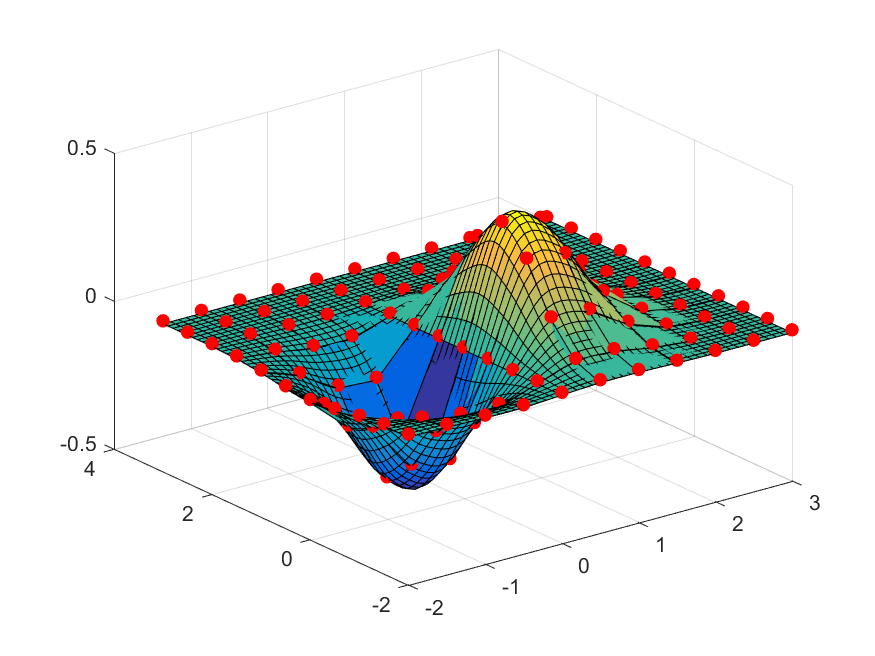
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 xx = -2 :0.5 :3 ; yy =xx; [X Y] = meshgrid (xx, yy); Z = X.*exp (-X.^2 -Y.^2 ); surf(X, Y, Z); hold onplot3 (X, Y, Z+0.01 , 'ro' , 'markerfacecolor' , 'r' );xx_i = -2 :0.1 :3 ; yy_i = xx_i; [X_i, Y_i] = meshgrid (xx_i, yy_i); Z_i = interp2(xx, yy, Z, X_i, Y_i); surf(X_i, Y_i, Z_i); hold offrotate3d on
如果要用spline光滑的内插,那么就要在interp2最后的参数写上’cubic’:
1 Z_i = interp2(xx, yy, Z, X_i, Y_i, 'cubic' );
此篇章结束,你真厉害!