matlab中的图像处理

（台湾人好像把图片称作影像捏）

imread() & imshow()

要对图片进行处理，当然第一步是读入图片了。matlab中使用imread方法读入图片，图片在matlab中将以矩阵的方式呈现。

读入之后，可以使用imshow方法显示读入的图片。

1
2
3

img1=imread('test image/lena.tif');
figure
imshow(img1)

whos

关键字whos可以把现在工作区中的变量详细的展示出来，例如对于图片来说，whos可以显示变量的名字，它的size、数据类型以及它的占用空间大小。如果要展示简单的信息则使用关键字who。

imageinfo()和imtool()

对于图片类型来说，使用imageinfo方法可以更加详细且有针对性地展示某个图片的信息。而imtool方法则会为用户弹出一个内置的工具界面，里面可以使用图形化的按钮去对图片进行处理。

1 2	imageinfo('test image/lena.tif') imtool('test image/lena.tif')

处理方法

immultiply()

immultiply方法的作用是将图像的亮度整体乘以一个常数。可以将图像变亮变暗。

img1=imread('test image/lena.tif');
img2=immultiply(img1, 1.5);
figure
subplot(1,2,1); imshow(img1);
subplot(1,2,2); imshow(img2);

imadd()

imadd方法是将两张图像相叠加。但是同样的，由于图像叠加后，整体的亮度对于两张原图来说都提升了，所以将会变亮。

img1=imread('test image/lena.tif');
img2=imread('test image/plane.tif');
img4=imadd(img1, img2);
figure
subplot(1,3,1); imshow(img1);
subplot(1,3,2); imshow(img2);
subplot(1,3,3); imshow(img4);

imhist()

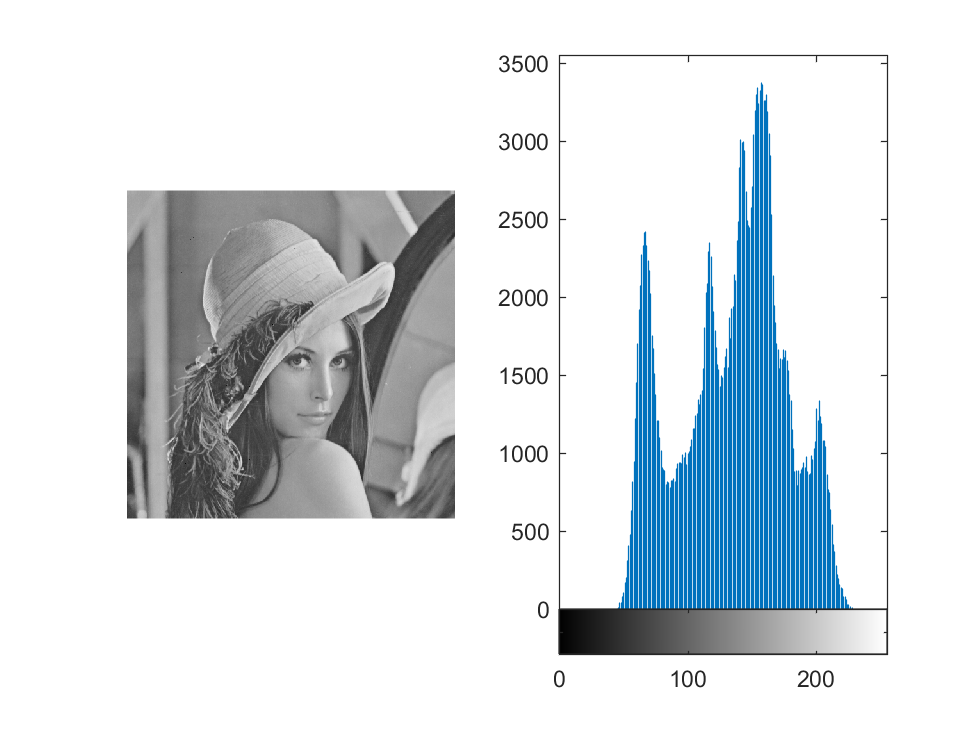
imhist可以展示出图片的直方图。

1 2	subplot(1,2,1); imshow(img1); subplot(1,2,2);imhist(img1);

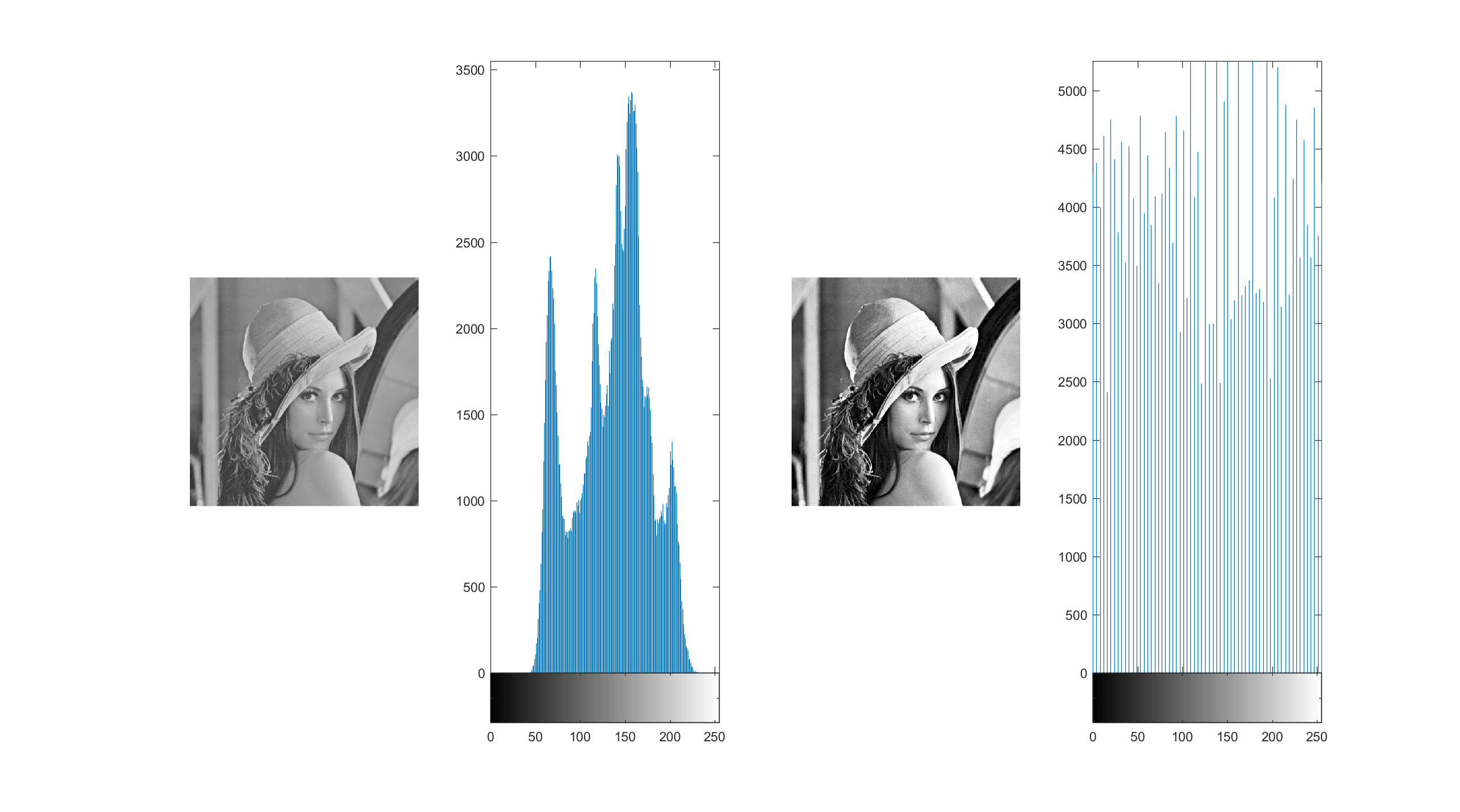
histeq()

histeq方法是对直方图做均衡化。这样原图灰度相差就会变大，形成一种对比度变大的感觉。

subplot(1,4,1); imshow(img1);
subplot(1,4,2); imhist(img1);
img1eq=histeq(img1);
subplot(1,4,3); imshow(img1eq);
subplot(1,4,4); imhist(img1eq);

myhisteq()

在课程中，老师让同学自己用代码实现一下直方图均衡化，在知道数学原理和算法之后，这个练习也并不复杂，但是步骤还是比较多的，这里给出一个下一篇博客的链接，在那里我会更加详细地完成这个练习。直方图均衡化

几何变换（geometric transformation）

常见的几何变换共有以下几种：

平移（translation）
放缩/拉伸（scale）
旋转（rotation）
切变（shear）
透视（perspective）

每一个几何变换对应一个变换矩阵。

scale

scale的变换矩阵为：

$\begin{bmatrix} S_x & 0 \\ 0 & S_y \end{bmatrix}$

作用到像素点：

$\begin{bmatrix} x'=S_xx \\ y'=S_yy \end{bmatrix} = \begin{bmatrix} S_x & 0 \\ 0 & S_y \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$

rotation

rotation有两种变换方向，顺时针和逆时针，当然两者本质上是互通的。逆时针旋转的变换矩阵为：

$\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}$

顺时针旋转的变换矩阵为：

$\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}$

给出推导过程：

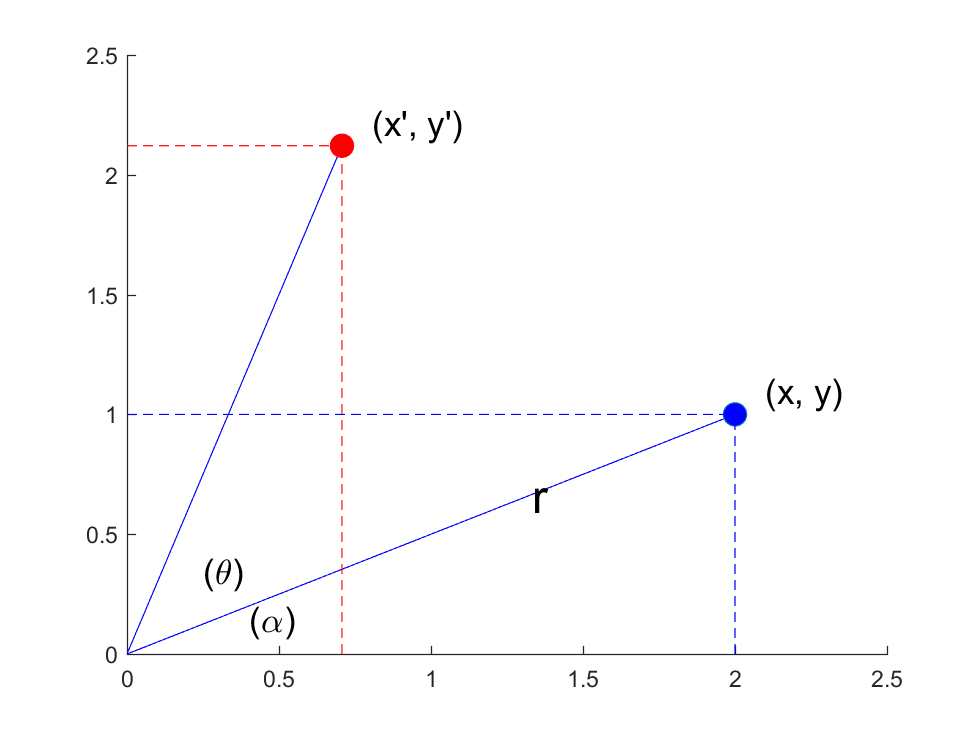
设初始点为 $(x, y)$ ，旋转后点为 $(x',y')$ ，半径为 $r$ ，旋转矩阵为 $\begin{bmatrix} a & b \\ c & d \end{bmatrix}$ 初始夹角为 $\alpha$ ，旋转角为 $\theta$ 。则可以列式：

$\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} x' \\ y' \end{bmatrix}$

$(x, y)=(rcos\alpha, rsin\alpha) \\ (x', y')=(rcos(\alpha+\theta), rsin(\alpha+\theta))$

带入得联立方程式：

$\begin{cases} arcos\alpha+brsin\alpha=rcos(\alpha+\theta) \\ crcos\alpha+drsin\alpha=rsin(\alpha+\theta) \end{cases}$

化简、展开

$\begin{cases} acos\alpha+bsin\alpha=cos(\alpha)cos(\theta)-sin(\theta)sin(\alpha) \\ ccos\alpha+dsin\alpha=sin(\alpha)cos(\theta)+cos(\theta)cos(\alpha) \end{cases}$

所以：

$a=cos\theta;b=-sin\theta;c=sin\theta;d=cos\theta$

顺时针情况下类似。值得一提的是，在matlab中有一个内置的函数imrotate()，其默认是顺时针方向旋转。

shear

shear的变换矩阵为：

$\begin{bmatrix} 1 & h_x \\ h_y & 1 \end{bmatrix}$

translation

终于讲到最简单却也是最特殊的变换，平移了。平面中，如果我们仍然要通过左乘变换矩阵的方式进行变换，那么平移的变换矩阵必须是三阶的

translation的变换矩阵为：

$\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}$

作用到像素点：

$\begin{bmatrix} x'=x+t_x \\ y'=y+t_y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}$

我曾经深刻地思考过这个问题，为什么就平移非得用三阶矩阵表示呢。最后我想到了一种解释。

拿一个矩形为例子，其实除了平移以外的变化，都是对这个矩形自身的改变，我们不用考虑到其他物体，只需要对这个矩形自身放大缩小旋转拉伸即可，而平移不是，平移是要有参照物的，需要考虑的是一种空间位置关系，没有别的参照物，你怎么知道它“平移”了？所以，第三维实际上就是潜在地给这个矩形加了一个坐标系，让它处于三维的“环境空间”中了。其实可以把第三维的1看成高度，现在这个矩形，默认处在空间中，其与xOy平行，且高度值z=1，这样是不是很容易理解！

因此，为了统一所有的变换，所有变换矩阵都用三阶来表示了，这样在做乘法的时候得以统一。

$scale=\begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} ; rotation=\begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \end{bmatrix}$

$shear=\begin{bmatrix} 1 & h_x & 0\\ h_y & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}; translation=\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix}$

perspective

透视变换较为复杂，这里仅给出其变换矩阵：

$perspective=\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & 1 \end{bmatrix}$

此小节结束，你真厉害！