直方图均衡化

直方图均衡化在网络上有相当多的博客，CSDN有许多优秀的回答，读者可自行查询。本博客主要从直方图均衡化的数学原理入手，主要参考了这一篇博客：直方图均衡化的数学原理

直方图均衡化，实际上是我们需要考虑如下图的方式：如何把一个凹凸不平的函数给尽量抹平。

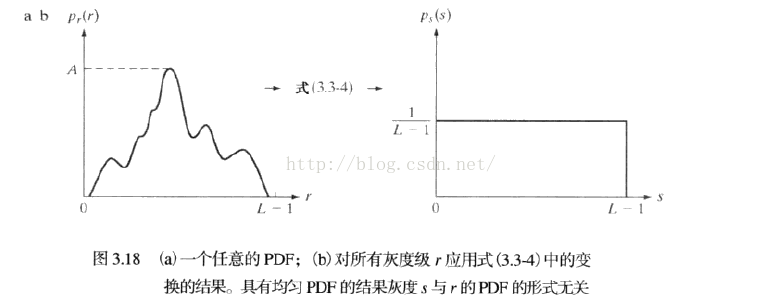
直方图的定义

由于我们平时遇到的直方图都是离散的，毕竟是像素统计出来的，但实际上我们可以先考虑连续情况，再推广到离散情况。

一个灰度级在范围[0, L-1]的数字图像，其直方图是一个离散函数

p(rk)=nknp(r_k)=\frac{n_k}{n}

n是图像的像素总数，nkn_k是图像中第k个灰度级的像素总数，rkr_k是第k个灰度级，k=0,1,2……L-1。这里我们对每一个nk都除以n是为了归一化，这样的画，函数与x轴包围的面积就是1。

直方图变换理论基础

设连续图像的概率分布为：

P(r)=lim⁡Δr→0A(r+Δr)−A(r)ΔrAP(r)=\lim_{\Delta r \rightarrow 0}\frac{A(r+\Delta r)-A(r)}{\Delta r A}

∫rminrmaxP(r)dr=1\int_{r_{min}}^{r_{max}}P(r)dr=1

r表示灰度，且0<=r<=1，A为图像面积。想象一下，图像面积随着x轴增大不断增加，当x=a时，图像面积的概率就是当x=a时面积的导数除以整个图像的面积。

对于离散图像的情况更简单一点：

P(ri)=ninP(r_i)=\frac{n_i}{n}

∑i=0k−1P(ri)=1\sum_{i=0}^{k-1}P(r_i)=1

假设r是原函数，s是均衡化后的函数，我们的任务目标就是找到一个灰度映射关系T，使s=T(r)s=T(r).

那么T的反变换就是 r=T−1(s)r=T^{-1}(s)

由概率论知，若Pr(r)P_r(r)和变换函数s=T(r)s=T(r)已知，r=T−1(s)r=T^{-1}(s)是单调增长函数，则变换后的图像灰度级的概率密度函数Ps(s)P_s(s)如下：

Ps(s)=(Pr(r)drds)∣r=T−1(s)P_s(s)=(P_r(r)\frac{dr}{ds})|_{r=T^{-1}(s)}

所以，现在的目标就是找到T

概率论——随机变量函数分布

T是r的累计分布函数

实际上，根据概率论中分布函数的知识，我们可以知道，T就是r的累计分布函数，这样就能抹平r。

s=T(r)=∫0rpr(ω)dωs=T(r)=\int_0^r p_r(\omega)d\omega

因为累计分布函数意味着每个灰度值占据总体像素的比例，只要这个比例作用到数轴上，那么就可以“拉伸”函数的各处，把它拉平。

想象一根皮筋，有的地方紧（表示比例多），有的地方松（表示比例少），现在我们拉这个皮筋要让它各处松紧程度一样，那是不是紧的地方拉长一点，松的地方拉少一点，一个道理。

推广到离散形式

设一副图像像素数为n，有l个灰度级，则第k个灰度级出现的概率可表示为：

Pr(rk)=nkn,0≤rk≤1,k=0,1,…,l−1P_r(r_k)=\frac{n_k}{n},0\leq r_k\leq 1, k=0,1,\dots,l-1

变换函数T（r）可改写为：

sk=T(rk)=∑j−0kPr(rj)=∑j=0knjn,0≤rk≤1,k=0,1,…,l−1s_k=T(r_k)=\sum_{j-0}^kP_r(r_j)=\sum_{j=0}^k\frac{n_j}{n},0\leq r_k\leq 1,k=0,1,\dots,l-1

例子

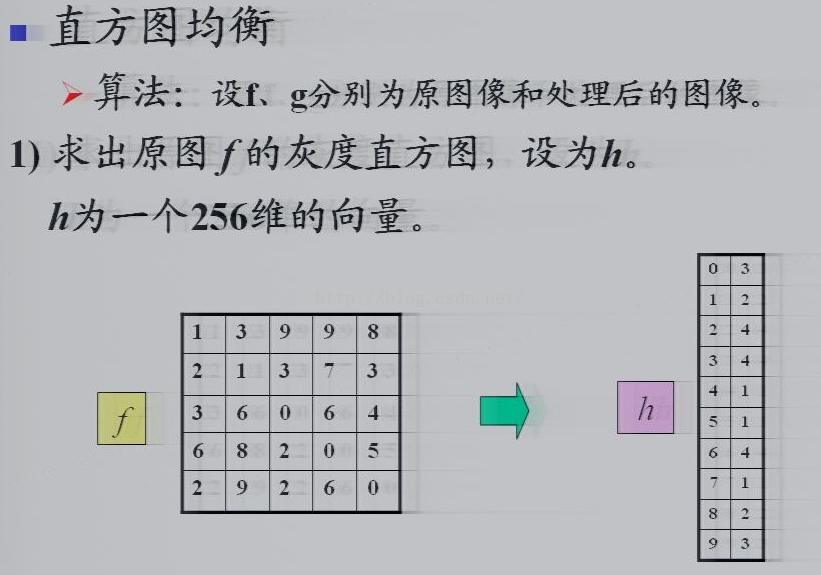
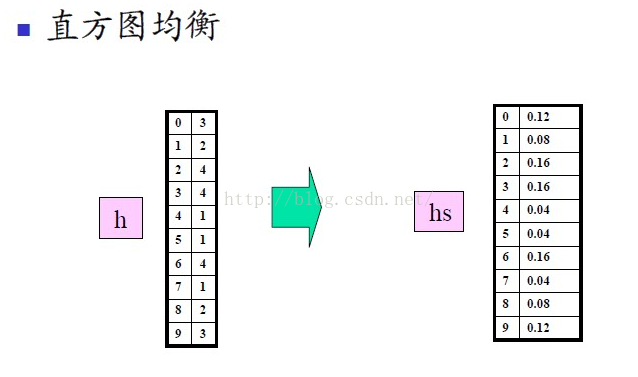
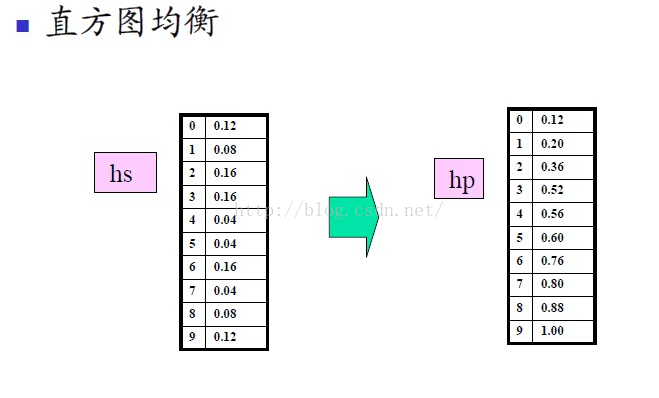
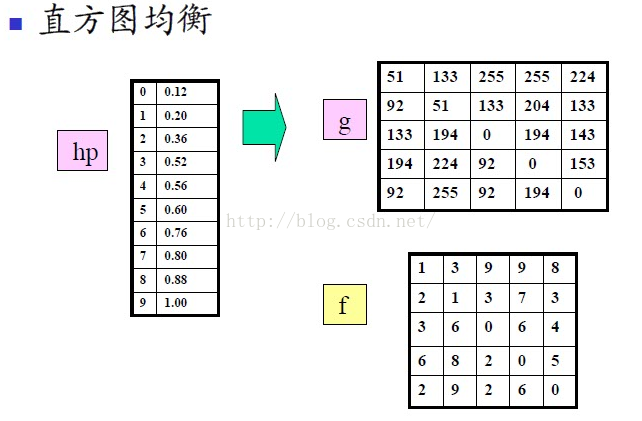
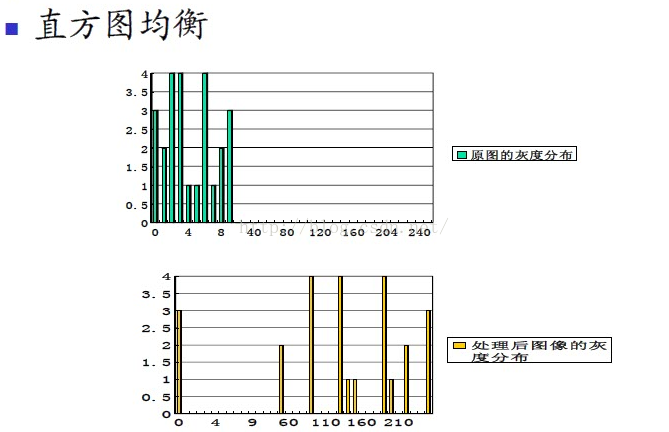
算法

1
2
3
4
5
6
7
8
9
10
%% 读入图片
img1=imread('test image/lena.tif');

% 直方图均衡化
after = myhisteq(img1);
figure
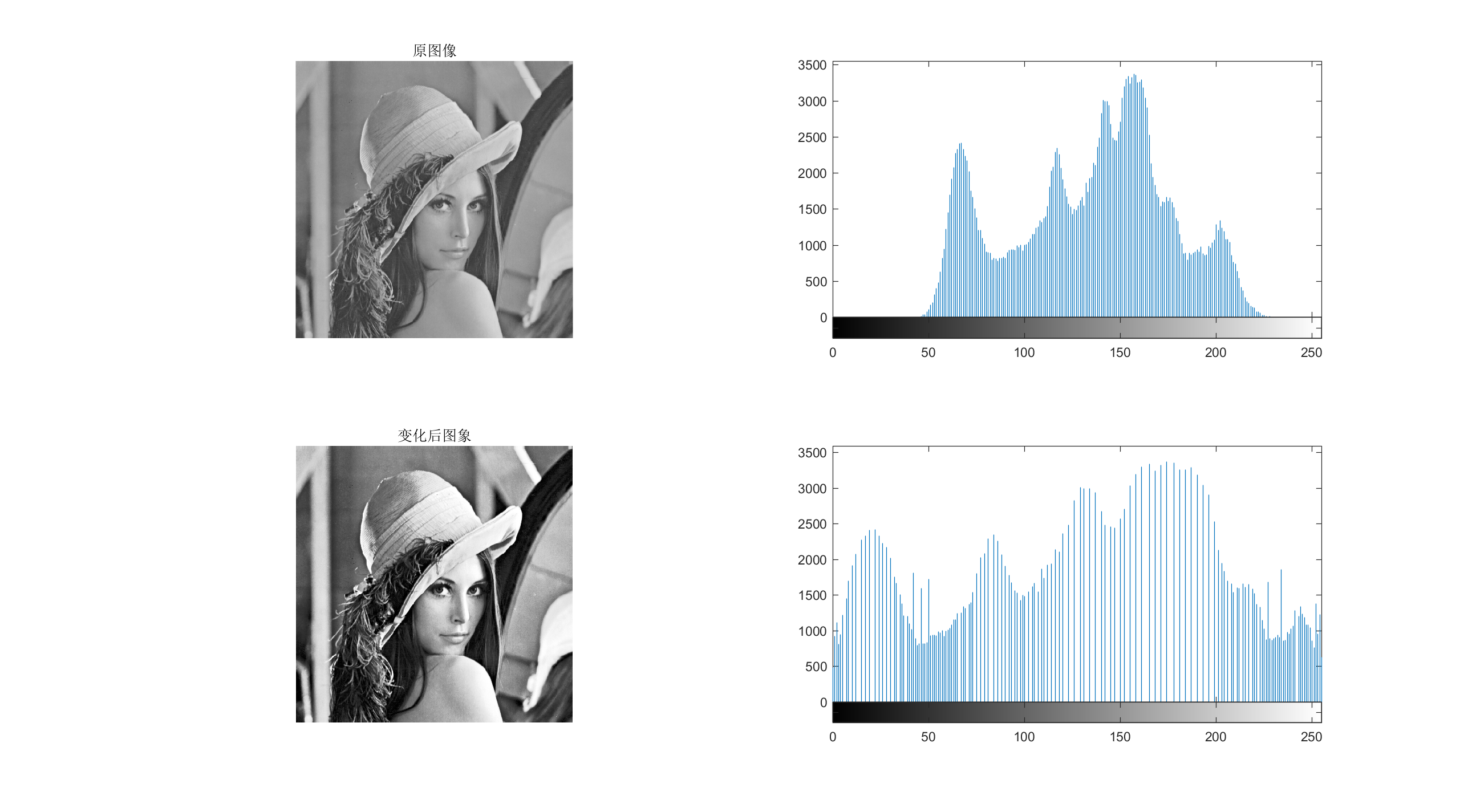
subplot(2,2,1); imshow(img1); title('原图像');
subplot(2,2,2); imhist(img1);
subplot(2,2,3); imshow(after); title('变化后图象');
subplot(2,2,4); imhist(after);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
% 函数
function hist_img = myhisteq( img1 )
% myhisteq 此处显示有关此函数的摘要
%   自己写的直方图均衡化

[height, weight] = size(img1);
img_size = height * weight; % 像素个数
hist_freq = zeros(1, 256); % 存储灰度分布
hist_freq_output = hist_freq; % 输出分布表

% 整理数据
temp = img1(:);
temp = sort(temp);

% 统计分布
for i = 1:img_size
    hist_freq(temp(i)+1) = hist_freq(temp(i)+1)+1; % hist_freq(1)灰度值为0
end

% 获得累计分布函数
hist_add_freq = hist_freq; % 先初始化到和分布函数相同
for i =2:256
    hist_add_freq(i) = hist_add_freq(i-1)+hist_freq(i);
end

for i = 2:256 % 初始化时fist_freq_output(1)=0
    hist_freq_output(i)=round(hist_add_freq(i)/img_size*255);
end

% 变换应用到图像
for i = 1:height
    for j = 1:weight
        img1(i, j) = hist_freq_output(img1(i, j)+1);
    end
end
hist_img = img1;

end

最后结果如图：