推荐系统(2)
基于近邻的协同过滤(Neighborhood-Based Collaborative Filtering)
基于近邻的协同过滤算法, 也被称为基于内存的算法(memory-based algorithm),是最早的为协同过滤而开发的算法之一。这类算法是基于相似的用户以相似的行为模式对物品进行评分, 并且相似的物品往往获得相似的评分这一事实。基于近邻的算法分为以下两个基本类型:
- 基于用户的协同过滤:这种类型中,把与目标用户A相似的用户的评分用来为A进行推荐。
- 基于物品的协同过滤:为了推荐目标物品B, 首先确定一个物品集合S, 使S中的物品与B相似度最高。
基于用户的协同过滤与基于物品的协同过滤的一个重要区别是: **前者利用相似用户的评分来预测该用户的评分;后者利用用户自己对相似物品的评分来预测用户对其他物品的评分。**前者利用用户(评分矩阵的行)之间的相似性来定义近邻;后者利用物品(评分矩阵的列)之间的相似性定义近邻。因此,这两种方法是互补的关系。
现在我们创建一个用户对于物品的评分矩阵,表头为项目编号,左侧第一列为用户编号。
| item1 | item2 | item3 | item4 | item5 | |
|---|---|---|---|---|---|
| user1 | 1 | 3 | 6 | ||
| user2 | 5 | 3 | 4 | ||
| user3 | 5 | 2 | 1 | 2 | 2 |
- 在实际情况中,这个表一般会有很多行很多列,非常庞大,而且是稀疏(有很多空数据),接下来我们要做的事情,就是对这个稀疏矩阵做处理。
评分矩阵的关键性质
我们假设R代表 m X n 的评分矩阵,其中m表示用户数, n表示物品数, ruj表示用户u对物品j的评分。矩阵中只有小部分数据是已知的,我们称已知的数据为训练数据,未知的数据为测试数据。
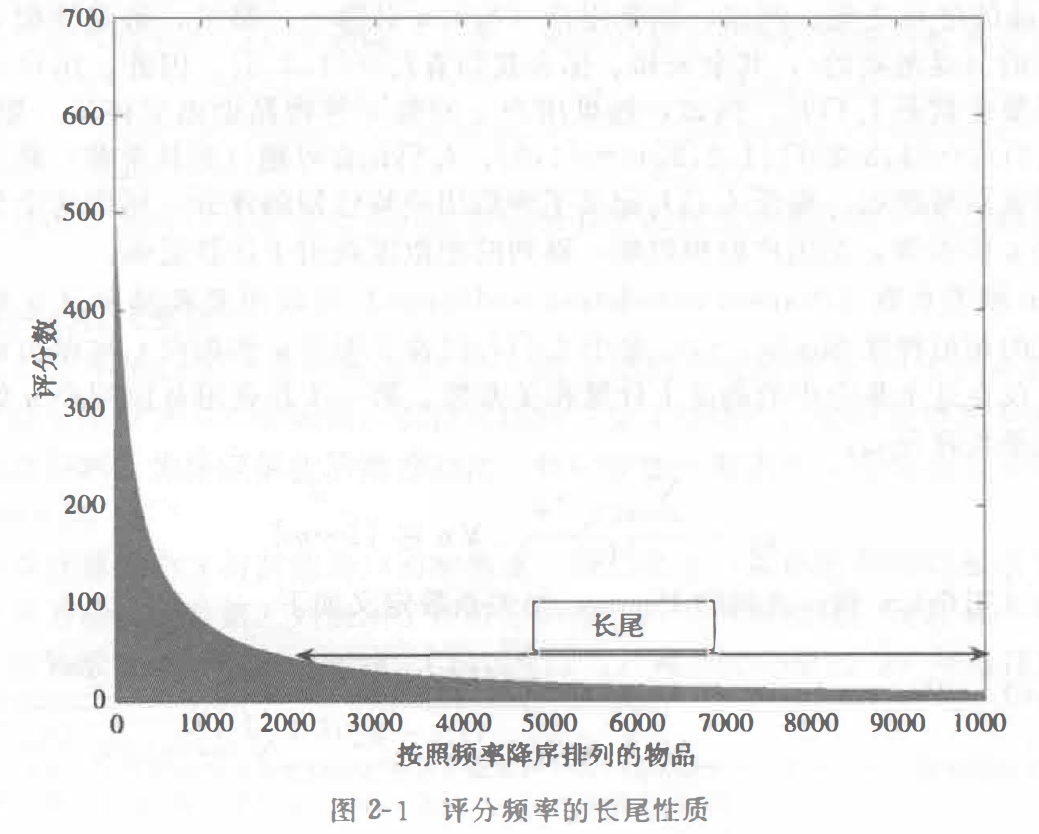
长尾性(long-tail)
物品评分的分布常常满足现实世界中的长尾(long-tail) 属性。这个名字是一个非常形象的表述。在现实情况中,只有一小部分商品会被高频率的评价,或者被点击,也就是所谓的爆款商品,然而,大部分的商品,也许和爆款商品类似,但是只能被大数据埋没在海面之下。当我们把商品和其被关注的频率画成一张表格的时候,“长尾性”就体现出来了。
如图,X轴表示物品的序号,Y轴表示被关注的程度。看来大部分商品都没有被关注呀!
通过基于近邻的方法预测评分
基于用户的邻近模型
首先是“基于用户的邻近模型”。我们来总结一下我们要做的事。
- 目标:预测评分矩阵中空的数据部分
- 方法:以一个用户A为基准,寻找和用户A相似的其他用户BCD…,寻找规律预测BCD…对项目的评分
为了方便理解,我们举一个实例。下面我来构建一个表格,表示各个用户对电影的评分,评分为10分制。
定义一个矩阵R:
| item1 | item2 | item3 | item4 | item5 | item6 | |
|---|---|---|---|---|---|---|
| user1 | 7 | 6 | 7 | 4 | 5 | 4 |
| user2 | 6 | 7 | ? | 4 | 3 | 4 |
| user3 | ? | 3 | 3 | 1 | 1 | ? |
| user4 | 1 | 2 | 2 | 3 | 3 | 4 |
| user5 | 1 | ? | 1 | 2 | 3 | 3 |
根据我们上述的“方法”,我们需要知道两个用户之间有多相似,“相似”这个东西总不是你说说相似就相似吧,所以我们需要一个数学方法,来讲两个用户之间的相似度定量表示出来。以下就是最经典的方法:
step1: 对于拥有m位用户和n件物品的mXn的评分矩阵 , 表示已经被用户u评价的物品的序号之集合。注意,是序号。
例如,user1和user2的I:
所以,我们可以得到两位用户之间共同评价的物品的列表集合:
我们需要用一个Pearson相关系数(Pearson correlation coefficient)来衡量用户u和用户v之间评分向量的相似程度,那么,如何计算Pearson相关系数呢?
step2:利用每位用户u的评分计算每位用户的平均评分
例如,计算user1的:
step3:接下来,user u和v之间的Pearson相关系数定义如下:
例如,我们来计算一下user1和user2的皮尔逊相关系数。
首先,
然后,
- 严格来说, 传统意义上的Pearson(u, v) 要求仅对用户u和用户v均做出评分的物品计算均值。也就是说上面的 将会变成 , 很难说哪种方法是比较好的方法,但是,我们考虑,如果两个用户的共同评价集合中只有一个共同元素时,Pearson系数就有点没意义了。
step4:接下来我们还要对用户的评分矩阵按行进行均值中心化,均值中心化就是把原先的矩阵都减去均值。例如:
| item1 | item2 | item3 | item4 | item5 | item6 | 均值 | |
|---|---|---|---|---|---|---|---|
| user1 | 7 | 6 | 7 | 4 | 5 | 4 | 5.5 |
| user2 | 6 | 7 | ? | 4 | 3 | 4 | 4.8 |
| user3 | ? | 3 | 3 | 1 | 1 | ? | 2 |
| user4 | 1 | 2 | 2 | 3 | 3 | 4 | 2.5 |
| user5 | 1 | ? | 1 | 2 | 3 | 3 | 2 |
| item1 | item2 | item3 | item4 | item5 | item6 | |
|---|---|---|---|---|---|---|
| user1 | 1.5 | 0.5 | 1.5 | -1.5 | -0.5 | -1.5 |
| user2 | 1.2 | 2.2 | ? | -0.8 | -1.8 | -0.8 |
| user3 | ? | 1 | 1 | -1 | -1 | ? |
| user4 | -1.5 | -0.5 | -0.5 | 0.5 | 0.5 | 1.5 |
| user5 | -1 | ? | -1 | 0 | 1 | 1 |
- 为什么要这么做呢?其实找相似度的感觉,可以理解成两个函数长得像不像,如果两条曲线重合,那么他们就一样,就是完全相似,但是如果有一条线上下平移一下呢?他们形状还是一样,但是相当于说,一个人整体给高分(是个好人),一个人整体给低分(是个坏人),这时候如果不均值化,当我们把好人的权重给坏人的时候,显然,坏人就打高分了,所以,这就是均值化的原因
用户u对物品j按均值中心化后的评分.被定义为原始评分减去其平均评分。
step5:令表示与目标用户u最相近的K位对物品做出评分的用户集合,一般相关为负数的都不会纳入其中。终于,整体的基于近邻的预测函数诞生了!
例如,现在我们要求,我们首先算出user3和所有用户的皮尔逊相关系数。如表:
| item1 | item2 | item3 | item4 | item5 | item6 | 均值 | 皮尔逊相关系数 | |
|---|---|---|---|---|---|---|---|---|
| user1 | 7 | 6 | 7 | 4 | 5 | 4 | 5.5 | 0.894 |
| user2 | 6 | 7 | ? | 4 | 3 | 4 | 4.8 | 0.939 |
| user3 | ? | 3 | 3 | 1 | 1 | ? | 2 | 1 |
| user4 | 1 | 2 | 2 | 3 | 3 | 4 | 2.5 | -1 |
| user5 | 1 | ? | 1 | 2 | 3 | 3 | 2 | -0.817 |
所以我们取user1和user2的数据集来计算(相关系数大于0)
然后我们要使用均值化的数据。
| item1 | item2 | item3 | item4 | item5 | item6 | |
|---|---|---|---|---|---|---|
| user1 | 1.5 | 0.5 | 1.5 | -1.5 | -0.5 | -1.5 |
| user2 | 1.2 | 2.2 | ? | -0.8 | -1.8 | -0.8 |
| user3 | ? | 1 | 1 | -1 | -1 | ? |
| user4 | -1.5 | -0.5 | -0.5 | 0.5 | 0.5 | 1.5 |
| user5 | -1 | ? | -1 | 0 | 1 | 1 |
- 当然其实还有最后一步,因为评分标准是没有小数的,所以就用四舍五入,化为整数(严谨!)
相似函数的一些变形
在实践中也会用到一些不同形式的相似度函数。一种变形是将余弦函数应用在原始评分上, 而不是应用在均值中心化的评分上:
那上面的例子,这样计算的话:
在余弦函数的一些实现中,分母上的归一化因子被设为基于该用户所有已评分的物品而不是两个用户共同已评分的物品:
那上面的例子,这样计算的话:
- 不过这些变化基本都没有皮尔逊相关系数常用。
相似度函数Sim (u, v)的可靠程度通常受用户u和用户v之间共有评分数量的影响。当两位用户的共有评分很少时,为了削弱这对用户的重要程度,应该引入一个削减因子以降低相似度。这种方法被称为显著性加权(significance weighting)
当两位用户的共有评价数小于特定的阈值β时,削减因子将被引入。削减因子的值定义为,显然,他的取值在[0,1],因此,削减过的相似度DiscountedSim (u, v)
定义如下:
假设我们定义β为5,那么我们发现user1和user3只有4项共同评价项目,这个时候相似度就要加一个权重咯(哼,只有四项共同评价,太少了吧!)
所以:
长尾的影响
在许多真实的场景中. 评分的分布通常呈长尾分布。某些电影可能非常受欢迎以至千它们经常作为被不同用户共同评价的项出现。这样的评价有时会降低推荐的质址、因为它们对不同的用户缺乏区分力。这与在文档检索应用中很常见并且无具体信息的单词(例如,“a” “ an” “the” )会使检索结果变坏的道理一样。因此,协同过滤中推荐的解决方法也与信息检索中的方法类似。正如信息检索中逆文档频率(idf) 这一概念一样,我们可以使用逆用户频率这一概念。设为物品)的评价数,m为用户总数,那么物品j的权重定义如下:
例如,对Pearson系数做如下修改以包含这些权重:
- 也就是说,评价数越多,物品的权重越小
基于物品的近邻模型
在基于物品的模型中,以物品而不是用户构建同组群体。因此,需要计算物品(即评分矩阵的列)之间的相似度。在计算列之间的相似度之前,每行的评分被以均值为零点中心化。和基于用户的模型一样.每一件物品的评分都被减去该物品的平均评分以得到一个
均值中心化的矩阵。
在基于物品的方法中仍然可以使用Pearson相关系数,但调整余弦通常会产生更好的结果。
所以,列的相似系数定义为:
我们来计算一下AdjustedCosine(1,3)
| item1 | item2 | item3 | item4 | item5 | item6 | |
|---|---|---|---|---|---|---|
| user1 | 1.5 | 0.5 | 1.5 | -1.5 | -0.5 | -1.5 |
| user2 | 1.2 | 2.2 | ? | -0.8 | -1.8 | -0.8 |
| user3 | ? | 1 | 1 | -1 | -1 | ? |
| user4 | -1.5 | -0.5 | -0.5 | 0.5 | 0.5 | 1.5 |
| user5 | -1 | ? | -1 | 0 | 1 | 1 |
后面的步骤类似,就是找K个最相关的,再作为权重……
降维与近邻方法
降维方法能够同时提高近邻方法的质量和效率。尤其是在稀疏矩阵中很难健壮地计算每对之间的相似度的情况下,降维也能够根据潜在因子提供稠密的低维表示。因此,这样的模型被称为潜在因子模型。即使两位用户共同评价过的物品很少,也能够计算其低维潜在向量之间的距离。更进一步,这种方法利用低维潜在向量决定同组群体也更有效率。
处理偏差
假设我们现在有三部电影,观众对这三部电影评价如下:
| 用户↓ | godfather | gladiator | nero |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 7 | 7 | 7 |
| 3 | 3 | 1 | 1 |
| 4 | 5 | 7 | 7 |
| 5 | 3 | 1 | ? |
| 6 | 5 | 7 | ? |
| 7 | 3 | 1 | ? |
| 8 | 5 | 7 | ? |
| 9 | 3 | 1 | ? |
| 10 | 5 | 7 | ? |
| 11 | 3 | 1 | ? |
| 12 | 5 | 7 | ? |
本例中, 评分范围为1~7, 由一组4个用户对3部电影的评价组成。显然,《Gladiator》和《Nero》之间的关联度非常高, 因为在已有的用户评分中. 它们的评分结果非常相似。《Godfather》和《Gladiator》之间的关联似乎不是很明显。但是, 有很多用户没有对《Nero》做出评分。由千《Nero》的平均得分为(0+1+1+7)/4 =4. 所以这些未知的评分被4代替。这些新项的加入明显降低了《Gladiator》和《Nero》之间的协方差。然而新添加的项对《Godfather》和《Gladiator》之间的协方差没有影响.
我写了一个计算协方差的代码
1 | // 计算协方差 |
得到的三部电影间协方差表格是:
| Godfather | Gladiator | Nero | |
|---|---|---|---|
| Godfather | 2.55 | 4.36 | 2.18 |
| Gladiator | 4.36 | 9.82 | 3.27 |
| Nero | 2.18 | 3.27 | 3.27 |
根据上面的估计, 《Godfather》和《Gladiator》之间的协方差大千《Gladiator》和Nero》之间的协方差。这看上去并不正确, 因为表2-3中,《Gladiator》和《Nero》的评分在两者都已知的评价中是一样的。因此《Gladiator》和《Nero》之间的协方差应该更高。这个偏差是使用平均值填充未知项造成的。这类偏差在稀疏矩阵中很重要, 因为其大部分项都是未知的。因此, 需要设计一种方法来降低用平均值代替未知项所带来的偏差。
我们可以用极大似然估计的方法来解决,其实很暴力,就是只看共同评价部分就好
极大似然估计法
每对物品之间的协方差仅使用巳知项进行估计。换句话说, 只有对某对物品做出评分的用户被用来估计协方差。
当没有用户在一对物品上做出共同评价时, 协方差被估计为0。使用这种方法, 协方差估计如下:
| Godfather | Gladiator | Nero | |
|---|---|---|---|
| Godfather | 2.55 | 4.36 | 8 |
| Gladiator | 4.36 | 9.82 | 12 |
| Nero | 8 | 12 | 12 |